难度说明：🟢简单🟡中等🔴困难

技巧篇

🟢01-只出现一次的数字（136）

1.题目内容

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间

示例 1 ：
输入：nums = [2,2,1]
输出：1

示例 2 ：
输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：
输入：nums = [1]
输出：1

2.题解思路

思路分析：基于这个题目有多种解题思路：

• 思路1（计数法）：通过哈希表存储每个数字的出现次数，然后再次遍历统计的数据得到出现一次的元素
• 思路2（标记法）：遍历数组，如果发现数据在集合中存在（说明存在重复），则从集合中移除这个数据，如果数据不存在则新加入集合，最终集合中留下来的就是只出现一次的元素
• 思路3（计算和）：因为题目具有特殊性，可以从数学角度进行切入，每个重复元素出现两次、某个不重复元素只出现一次，因此可以用集合中元素之和*2-数组之和=不重复元素，即先获取到所有元素，通过这个公式实现计算

👻方法1：暴力法（计数、标记去重）

/**
 * 136.只出现一次的数字
 * 暴力思路：
 * 计数法：遍历数组，统计数组元素出现次数，然后遍历统计数据获取到出现此处为1的元素
 * 标记法：遍历数组，如果发现数据在集合中存在（说明存在重复），则从集合中移除这个数据，如果数据不存在则新加入集合，最终集合中留下来的就是只出现一次的元素
 */
class Solution {

    // 思路1：计数法
    public int singleNumber1(int[] nums) {
        // 通过哈希表存储元素的出现次数
        HashMap<Integer,Integer> map = new HashMap();

        // 1.统计元素出现次数
        for (int num : nums) {
            // 判断数据是否存在
            if(map.containsKey(num)) {
                map.put(num,map.get(num)+1);
            }else{
                map.put(num,1);
            }
        }

        // 2.遍历统计数据
        Iterator<Integer> iterator = map.keySet().iterator();
        while(iterator.hasNext()) {
            int key = iterator.next();
            if(map.get(key)==1) {
                return key;
            }
        }
        return 0;
    }

    // 思路2：标记法(去重法)
    public int singleNumber2(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int num : nums) {
            // 判断当前数据是否存在在集合中
            if(set.contains(num)){
                // 从集合中移除重复的元素
                set.remove(num);
            }else{
                // 如果数据不存在，将当前节点加入集合
                set.add(num);
            }
        }
        // 最终集合中剩下的元素就是不重复的那个
        return set.iterator().next();
    }
}

复杂度分析

• 时间复杂度：
• 空间复杂度：

👻方法2：位运算

​ 此处运用到位运算的技巧，采用异或运算进行一次遍历解决

• 【1】任何数和0做异或运算还是原来的数：a⊕0=a
• 【2】任何数和其自身做异或运算，结果是 0：a⊕a=0
• 【3】异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b

​ 基于此，因为重复元素都是两个、不重复元素只有一个，因此可以用0去与数组中的每一个元素做异或操作，进而得到这个不重复元素

• 重复元素都是两个：通过【3】，其得到的结果必然是0
• 不重复元素只有一个：通过【1】，0和这个不重复元素做异或操作得到的必然是原数

复杂度分析

• 时间复杂度：
• 空间复杂度：

3.复盘

🟢02-多数元素（169）

1.题目内容

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素

2.题解思路

• 思路1（计数法）：类似地，统计元素出现次数，然后返回统计次数大于n/2的元素
• 思路2：

👻方法1：计数法

/**
 * 169.多数元素
 */
class Solution {
    public int majorityElement(int[] nums) {

        // 存储元素出现次数
        HashMap<Integer,Integer> map = new HashMap();

        // 存储满足条件的元素(此处题目返回是1个那就不用集合)

        // 统计元素出现次数
        for (int i = 0; i < nums.length; i++) {
            if(map.containsKey(nums[i])) {
                // 如果存在，计数+1
                map.put(nums[i],map.get(nums[i]) + 1);
            }else{
                map.put(nums[i],1);
            }
        }

        // 返回元素出现次数大于n/2的元素
        Iterator<Integer> iterator = map.keySet().iterator();
        while (iterator.hasNext()) {
            int key = iterator.next();
            if(map.get(key)>nums.length/2) {
                return key;
            }
        }

        return 0;
    }
}

​ 如果要基于上述思路优化，可以在遍历过程中每次都去更新下当前的最大值，最终返回这个最大值即可，基于此可以省去后面的遍历步骤

// 计数法优化
public int majorityElement2(int[] nums) {

    // 存储元素出现次数
    HashMap<Integer,Integer> map = new HashMap();

    // 因为返回值只有一个int，因此此处可以理解为找"最大值"（出现次数最多的元素,注意此处是返回元素，而不是元素出现次数）
    HashMap<String,Integer> max = new HashMap(); // max 只存储一组数据（maxItem,出现次数）或者拆开来存储（maxItem：xxx，count：xxx）
    max.put("maxItem",nums[0]);
    max.put("count",0);

    // 统计元素出现次数
    for (int i = 0; i < nums.length; i++) {
        if(map.containsKey(nums[i])) {
            int val = map.get(nums[i]) + 1;
            // 如果存在，计数+1
            map.put(nums[i],val);
            if(val > max.get("count")){
                // 更新
                max.put("maxItem",nums[i]);
                max.put("count",val);
            }
        }else{
            map.put(nums[i],1);
        }
    }

    return max.get("maxItem");
}

复杂度分析

• 时间复杂度：
• 空间复杂度：

👻方法2：排序法

​ 从题目中分析可以知道，此处找的是众数，因此可以采用排序的思路解决：如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为 ⌊2n⌋ 的元素（下标从 0 开始）一定是众数

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

🟡03-颜色分类（75）

1.题目内容

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地 对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题

2.题解思路

思路解析：

• 思路1（穷举遍历法）：既然已经知道了一共有3个颜色球，则可定义3个列表存储，然后按照指定顺序进行合并（但此处引用了原有的空间，不符合原地概念，且扩展性差）
• 思路2（排序）：既然不能使用内置的sort，那么就自己手撕排序算法实现排序（冒泡排序、快速排序等）
• 思路3（计数）：遍历数组元素，计算每个球的个数，然后重新填充数组

❌方法1：穷举遍历法

​ 既然已经知道了一共有3个颜色球，则可定义3个列表存储，然后按照指定顺序进行合并。（但此处引用了原有的空间，不符合原地概念）

public void sortColors(int[] nums) {
    List<Integer> red = new ArrayList<Integer>();
    List<Integer> white = new ArrayList<Integer>();
    List<Integer> blue = new ArrayList<Integer>();

    // 步骤1：遍历数组，存储各个颜色的小球到指定集合
    for (int num : nums) {
        switch (num) {
            case 0: {
                red.add(num);
                break;
            }
            case 1: {
                white.add(num);
                break;
            }
            case 2: {
                blue.add(num);
                break;
            }
        }
    }

    // 步骤2：合并最终的集合
    red.addAll(white);
    red.addAll(blue);
    for (int i = 0; i < red.size(); i++) {
        nums[i] = red.get(i);
    }
}

复杂度分析

• 时间复杂度：
• 空间复杂度：

👻方法2：手撕排序

​ 冒泡排序（双重遍历、依次交换）

// 冒泡排序（排序法）
public void sortColors(int[] nums) {
    for(int i=0;i<nums.length;i++) {
        for(int j=i+1;j<nums.length;j++) {
            if(nums[i]>nums[j]) {
                // 交换元素
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
    }
}

🟡04-下一个排列（31）

参考题解1：

1.题目内容

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

• 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

• 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
• 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
• 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须** 原地 **修改，只允许使用额外常数空间。

示例 1：
输入：nums = [1,2,3]
输出：[1,3,2]

示例 2：
输入：nums = [3,2,1]
输出：[1,2,3]

示例 3：
输入：nums = [1,1,5]
输出：[1,5,1]

2.题解思路

​ 结合题意分析，下一个序列的含义包含了两层内容：

• 将后面的大数与前面的小数进行交换，就能得到更大的数，例如123456中将5和6进行交换可以得到要给更大的数123465
  • 正向来说如果是正向递增顺序则序列是最小的，因此可以反向遍历找到第1个降序的位置 ，说明这个位置可以交换一个大数让数变大
• 让增加的幅度尽可能小，即要交换的大数要尽可能小，且交换后的大数后面的数字按照升序排序，就能得到一个排列最小的序列
  • 将一个尽可能小的大数和前面的小数进行交换
  • 交换后，将这个位置后面的序列进行升序排序（升序排列就是最小的排列）

​ 因此算法的实现思路可以从两点切入：

• 定位到可变大的位置：逆序找到第一个降序的序列
• 确定交换数字进行交换，随后将当前位置后面的序列进行升序

​ 以54876为例：

• 确定交换（可变大）位置：逆序遍历找到第1个降序序列48（4：对应[i-1]位置；8对应[i]位置）

• 交换大数：找到([i-1],length)序列中比nums[i-1]的大最小数（先升序排序，找到第一个比它大的数进行交换即可）

• 升序排列：再次对([i-1],length)进行排序（因为交换后原有的顺序就被打乱了，需要再次排序确保序列升序）

• 如果不存在下一个序列（即一开始就没有可交换的位置），则需要将其排为最小的序列（升序排序即可），因此要定义标识进行判断

👻中规中矩（按照查找下一个序列的思路）

• 确认交换位置（可变大的位置：即逆序遍历的第1个降序位置），记录索引
• 如果存在可交换的位置：
  • 找到当前位置后的找到比它大的数（即尽可能小的大数）进行交换（可以先升序排序，然后找到第1个比它大的数）
  • 交换完成后，需再次对当前交换位置后的序列进行升序排序（因为交换后原来的顺序就被打乱了，需重新排序确保得到尽可能小的序列）
• 如果不存在可交换的位置，说明当前序列最大了，直接升序排序返回

public void nextPermutation(int[] nums) {

    // 定义序列标识，是否存在下一个序列
    boolean flag = false;

    // 1.确定可变大的交换位置（逆序找到第一个降序序列）
    int swapIndex = -1;
    for (int i = nums.length - 1; i > 0; i--) {
        // 判断 i 与 i-1 是否出现降序，如果出现则说明此处i-1位置可以进行交换
        if (nums[i] > nums[i - 1]) {
            swapIndex = i - 1; // 此处为避免混乱，可记录可交换的位置swapIndex（即为对应i-1的位置）
            // 找到第一个降序序列就跳出循环，否则会影响执行流程（或者直接将后面的步骤放在这里执行）
            flag = true; // 表示存在可交换位置
            break;
        }
    }
    // 如果存在可交换位置
    if (flag) {
        // 2.对swapIndex之后的序列进行遍历，获取到尽可能小的大数进行交换（先升序排序，随后找到第一个比swapIndex大的数即可）
        Arrays.sort(nums, swapIndex + 1, nums.length);
        for (int j = swapIndex; j < nums.length; j++) {
            if (nums[j] > nums[swapIndex]) {
                // 将当前两个元素进行交换
                int temp = nums[swapIndex];
                nums[swapIndex] = nums[j];
                nums[j] = temp;
                // 操作完成跳出循环
                break;
            }
        }
        // 3.再次对交换位置后面的序列进行排序
        Arrays.sort(nums, swapIndex + 1, nums.length);
    } else {
        // 不存在下一个更大的序列，需重排为最小序列
        Arrays.sort(nums);
    }
}

👻其他参考方法：

复杂度分析

• 时间复杂度：
• 空间复杂度：

1. 找到第一个比后面小的元素
2. 与后面比它大的最小值交换
3. 交换后使他后面的数字升序排列, reverse即可, 因为 1. 的特性,后面是降序排列的

参考题解：

class Solution {
    public void nextPermutation(int[] nums) {
        int pre = nums.length - 2;
        while (pre >= 0 && nums[pre] >= nums[pre + 1]) pre--;
        if (pre == -1) reverse(nums, 0, nums.length - 1); // 边界值处理
        else {
            int post = pre + 1;
            while (post < nums.length && nums[post] > nums[pre]) post++;
            post--;
            int t = nums[pre];
            nums[pre] = nums[post];
            nums[post] = t;
            reverse(nums, pre + 1, nums.length - 1);
        }
    }
    void reverse(int[] nums, int l, int r) {
        while (l < r) {
            int t = nums[l];
            nums[l++] = nums[r];
            nums[r--] = t; 
        }
    }
}

参考题解：

1、[1,2,3,6,5,4]下一个排列是[1,2,4,3,5,6]完全题解题意后就好写了 2、从后往前找到不是递增的那个数上述是3，然后再从后往前找到第一个比3大的数，交换这两个数的位置后[1,2,4,6,5,3] 3、已近知道6,5,3从后往前是递增的，所以要逆序一下 4、注意边界判断

class Solution {
     public void nextPermutation(int[] nums) {
        if (nums == null || nums.length == 0) {
            return;
        }
        int i = nums.length - 2;
        while (i >= 0 && nums[i + 1] <= nums[i]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        }
        revers(nums, i + 1, nums.length - 1);
    }

    private void revers(int[] nums, int i, int j) {
        while (i < j) {
            swap(nums, i++, j--);
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

3.复盘

🟡05-寻找重复数（287）

1.题目内容

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

2.题解思路

​ 初步题解思路参考：排序、hash等方式，还有一种特殊方式是快慢指针

• abs 绝对值思路：将nums[i]的绝对值当作nums的下标，遍历一遍并给对应下标的值乘上-1，如果遇到小于0的值则寿命之前已经标记过了，对应下标就是重复的数（但是这种方案会修改nums[i]的值）
• 排序：排序数组，然后依次对比相邻两个元素的大小，如果相等则说明出现重复数字
• 计数：使用一个集合记录每个元素出现的次数，如果发现次数大于1则说明重复
• HashSet：HashSet存储的是无序的、不重复的元素，如果add失败则说明数据重复直接返回这个值即可

❌方法1：绝对值（标记法：需修改数组）

​ 涉及修改数组元素，不符合题意，但也是一种题解思路

public int findDuplicate(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        int index = Math.abs(nums[i]);
        // 判断是否小于0
        if(nums[index] < 0){
            return index;
        }else{
            nums[index] = -1 * nums[index]; // 标记数组元素
        }
    }
    return 0;
}

❌方法2：排序（需额外空间+修改数组）

// 排序：对数组元素进行排序，依次比较相邻两个元素是否相同，如果相同则说明有重复
public int findDuplicate(int[] nums) {
    // 排序
    Arrays.sort(nums);
    // 检验数组相邻两个元素是否相同
    for(int i=0;i<nums.length;i++){
        if(nums[i]==nums[nums[i]]){
            return nums[i];
        }
    }
    return -1;
}

❌方法3：计数（需额外空间）

// 计数：使用集合存储元素出现个数，遍历过程中判断次数是否大于1
public int findDuplicate3(int[] nums) {
    // 定义数组存储元素出现个数，其中下标为对应元素
    int[] count = new int[nums.length];
    for (int i = 0; i < nums.length; i++) {
        // 校验是否值是否大于1
        if(++count[nums[i]]>1){ // 等价于count[nums[i]]++,if(count[nums[i]]>1){...}
            return nums[i];
        }
    }
    return -1;
}

❌方法4：集合判断（HashSet、List）（需额外空间）

// 集合判断（list、hashset）或者校验集合中元素是否存在
public int findDuplicate4(int[] nums) {
    /*
        ArrayList<Integer> list = new ArrayList<Integer>();
        for (int i = 0; i < nums.length; i++) {
            if(list.contains(nums[i])) {
                return nums[i];
            }
            list.add(nums[i]);
        }
        return -1;
         */
    HashSet<Integer> set = new HashSet<Integer>();
    for (int i = 0; i < nums.length; i++) {
        if(!set.add(nums[i])) {  // 类似的，有set.contains(nums[i]);
            return nums[i];
        }
    }
    return -1;
}

❌方法5：暴力双重循环（依次比较元素，不需要额外空间、不用修改数组，但超时）

// 暴力循环（双层循环依次比较元素，有点类似冒泡的方向）
public int findDuplicate5(int[] nums) {
    for(int i = 0; i < nums.length; i++) {
        for(int j = i + 1; j < nums.length; j++) {
            if(nums[i] == nums[j]) {
                return nums[i];
            }
        }
    }
    return -1;
}

👻方法2：快慢指针

思路核心：考虑到题目提供数组的特殊性，此处可以三个指针的方式去做，先定义slow、fast指针敲定重复序列（环），然后再定义finder（起点）和slow指针一起走敲定环的入口

​ 基于环形链表的思路去实现，即理解如何将数组当作链表来处理。将数组中的元素，通过链表进行关联：

​ 1 3 4 2：用链表理解即为1->3->4->2，要判断是否存在重复数即判断链表是否存在环，这点基于链表的快慢指针思路可以实现。可以将这个特殊数组当作要给链表来看，数组的下标是指向该元素的指针，数组的元素也看作是指针

​ 例如0是指针，指向nums[0]，而nums[0]也是指针，指向nums[num[0]]

int point = 0;
while(true){
    point = nums[point]; // 等同于 next = next->next; 
}

​ 此处之所以可以基于此转化，是因为题目提供数组的特殊性

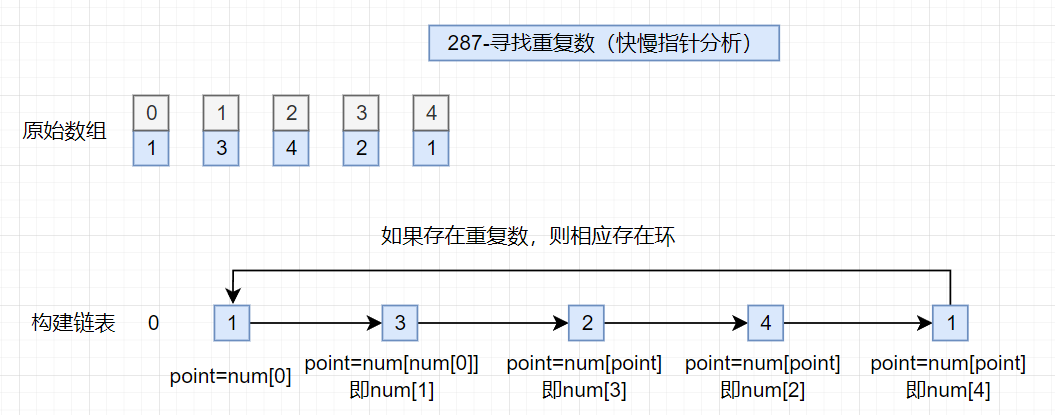
​ 类似地，基于此

​ 基于此可以将接替思路拆解为两步：以1 3 4 2 2为例子

• 存在环：通过快慢指针，如果指针指向重复的数字表示存在环
• 寻找环的入口：定义一个finder指针，它从起点开始和slow（slow、fast相遇处）同步前进，当finder和slower相遇则是在环的入口处相遇，即表示在重复数字相遇

public int findDuplicate(int[] nums) {

    // 定义快、慢指针
    int slow = 0,fast = 0;
    slow = nums[slow]; // 对应slow = slow.next （慢指针先走一步）
    fast = nums[nums[fast]];// 对应fast = fast.next.next (快指针先走两步)

    // 已知会存在环，slow和fast会在重复序列中相遇（因此当两者不相等的时候就继续走，直到相遇）
    while (fast != slow) {
        slow = nums[slow];
        fast = nums[nums[fast]];
    }

    // 定义finder指针和slow一起走，他们必定会在入口处相遇
    int finder=0;
    while(finder!=slow){
        finder = nums[finder];
        slow = nums[slow];
    }
    return slow; // finder
}

​ 上述写法等价于下面的：

public int findDuplicate(int[] nums) {

    // 定义快、慢指针
    int slow = 0,fast = 0;
    // 已知会存在环，slow和fast会在重复序列中相遇（因此当两者不相等的时候就继续走，直到相遇）
    while (true) {
        slow = nums[slow]; // 对应slow = slow.next （慢指针先走一步）
        fast = nums[nums[fast]]; // 对应fast = fast.next.next (快指针先走两步)
        if (slow == fast) {
            break;
        }
    }

    // 定义finder指针和slow一起走，他们必定会在入口处相遇
    int finder=0;
    while(true){
        finder = nums[finder];
        slow = nums[slow];
        if(finder==slow){
            return finder;
        }
    }
}

复杂度分析

• 时间复杂度：
• 空间复杂度：

3.复盘