难度说明：🟢简单🟡中等🔴困难

回溯

todo：回溯的解题技巧

什么情况下需要递归、回溯

算法核心步骤梳理

解题思路分析

常见题型说明

🟡01-全排列（46）

1.题目内容

​ 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

2.题解思路

参考题解

• 参考题解：计算全排列方法解析

​ 思路分析：对于一个长度为n的数组（假设元素互不重复），则其排列方案数共有n×(n−1)×(n−2)…×2×1个

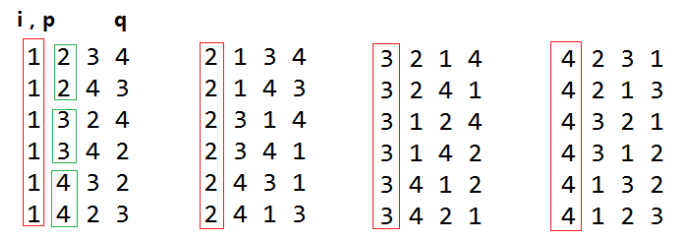
​ 排列方案分析：根据数组排列的特点，考虑深度优先搜索所有排列方案。即通过元素交换，先固定第 1 位元素（ n 种情况）、再固定第 2 位元素（ n−1 种情况）、... 、最后固定第 n 位元素（ 1 种情况）

👻方法1：递归

public class Solution {

    // 定义返回结果
    List<List<Integer>> res = new ArrayList<List<Integer>>();

    // 暴力思路：多层嵌套
    public List<List<Integer>> permute(int[] nums) {
        // 调用递归方法进行全排列（此处先将nums转化为List便于处理）
        List<Integer> numsList = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            numsList.add(nums[i]);
        }
        // 调用递归方法进行全排列
        dfs(numsList,0);
        // 返回结果
        return res;
    }

    // 定义两个元素交换的方法
    public void swap(List<Integer> nums, int i, int j) {
        int temp = nums.get(i);
        nums.set(i, nums.get(j));
        nums.set(j, temp);
    }

    // 定义dfs遍历方式
    public void dfs(List<Integer> nums, int x) {
        // 递归出口，遍历到数组尾部结束
        if (x == nums.size() - 1) {
            res.add(new ArrayList<>(nums)); // 添加排列方案(此处需new一个，否则添加的是引用)
            return; // 退出当前方法
        }
        // 执行操作
        for (int i = x; i < nums.size(); i++) {
            // 核心操作：交换（将nums[i]固定在x的位置）、进行全排列算法、复原（通过再次交换，还原成原来的数组便于下一次进行排列）
            swap(nums, i, x); // 交换
            dfs(nums, x + 1); // 进行全排列算法
            swap(nums, i,x); // 复原
        }
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

class Solution {
    List<Integer> nums;
    List<List<Integer>> res;

    void swap(int a, int b) {
        int tmp = nums.get(a);
        nums.set(a, nums.get(b));
        nums.set(b, tmp);
    }

    void dfs(int x) {
        if (x == nums.size() - 1) {
            res.add(new ArrayList<>(nums));  // 添加排列方案
            return;
        }
        for (int i = x; i < nums.size(); i++) {
            swap(i, x);              // 交换，将 nums[i] 固定在第 x 位
            dfs(x + 1);              // 开启固定第 x + 1 位元素
            swap(i, x);              // 恢复交换
        }
    }

    public List<List<Integer>> permute(int[] nums) {
        this.res = new ArrayList<>();
        this.nums = new ArrayList<>();
        for (int num : nums) {
            this.nums.add(num);
        }
        dfs(0);
        return res;
    }
}

👻方法2：

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡02-子集（78）

1.题目内容

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的

子集

（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

2.题解思路

👻方法1：回溯

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

class Solution {
    List<List<Integer>> res;
    List<Integer> list = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        res = new ArrayList<>();
        backTracing(nums, 0);
        return res;
    }
    public void backTracing(int[] nums, int start){
        // 每更新一次list  都加入结果集  首次进来加的是空集
        res.add(new ArrayList<>(list));
        // 到数组末尾结束当前递归
        if(start == nums.length){
            return;
        }
        for(int i = start; i < nums.length; i++){
            // 将当前数加入list
            list.add(nums[i]);
            // 递归 不能重复使用当前数 因此下一轮从i+1开始
            backTracing(nums, i+1);
            // 回溯 回退刚刚加的数
            list.remove(list.size()-1);
        }
    }
}

👻方法2：动态规划思路

​ 核心：在原有的子集中不断追加下一个元素构建成新的子集进行补充（可以结合测试用例进行理解）

​ nums大小不一定为0，解集中一开始只有空集，然后每遍历一个数字，就拷贝当前解集中的所有子集，然后基于此子集不断追加当前数字（即构成新的子集放入解集中），以此类推，直到所有数字遍历完成

​ 此处动态规划思路：包含当前数的子集组合=上一个数的获得的每一个子集组合+当前数。所有子集=遍历的每一个数的获得的子集组合的合集

/**
 * 78.子集
 */
public class Solution {

    // 核心：循环遍历数组元素，每遍历一个数字，就基于当前子集追加当前数字构成新的子集，进而进入下一个数字遍历，以此类推直到所有的数字遍历完成
    public List<List<Integer>> subsets(int[] nums) {
        // 定义结果集合
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        res.add(new ArrayList<>()); // 初始化加入空集（空集也是子集的一部分）
        // 依次遍历数字
        for (int i = 0; i < nums.length; i++) {
            // 计算当前子集大小，遍历每个子集，将元素进行追加并生成新的子集
            int size = res.size(); // 当前子集数
            for (int j = 0; j < size; j++) {
                List<Integer> temp = new ArrayList<>(res.get(j)); // copy一份子集
                temp.add(nums[i]); // 追加元素，生成新的子集
                res.add(temp); // 追加新子集
            }
        }
        return res;
    }

}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡03-电话号码的字母组合（17）

1.题目内容

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母

示例 1：

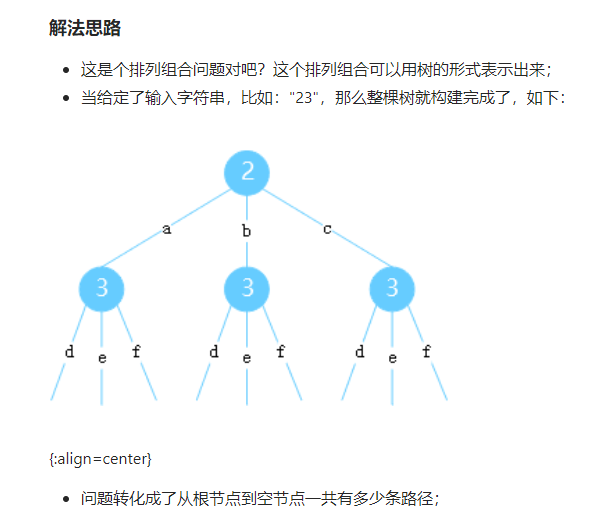
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

2.题解思路

​ 结合题意进行分析，首先需要存储数字对应的字母序列（可以使用类似数组映射的方式或者哈希表的方式）

• 方式1：数组映射，数字作为数组的下标索引，数组元素存储对应的字母序列
  • String[] letters = new String[]{"","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}
• 方式2：哈希表映射（HashMap存储）
  • Map<Character, String> phoneMap = new HashMap<Character,String>(){...}

​ 随后基于此构建回溯方法（在循环中嵌套了递归调用），可以通过穷举的方式去理解递归的演变

// 假设是"2345"数字序列，那么实际上就是通过构建多层遍历去实现字符串拼接，其实现参考如下
result = List()
for(i=0;i<len("abc");i+=1) {
    for(j=0;j<len("def");j+=1) {
        for(k=0;k<len("ghi");k+=1) {
            for(n=0;n<len("jkl");n+=1)
                tmp = i+j+k+n
                result.add(tmp)
        }
    }
}
return result

// 但显然，如果输入字符串长度不固定，则对应嵌套循环的层数也不固定，因此引入递归来实现

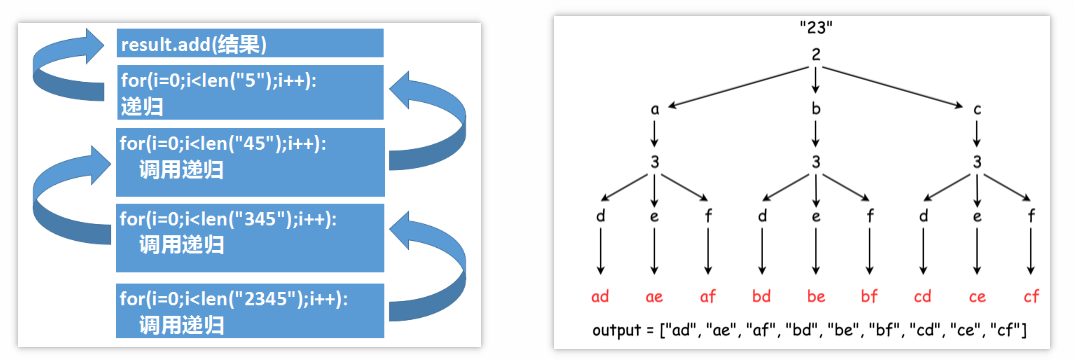
​ 对于打印"2345"这样的字符串：

• 第一次递归就是上图中最下面的方格，然后处理完第一个字符2之后，将输入的字符改变成"345"并调用第二个递归函数
• 第二次递归处理3，将字符串改变成"45"后再次递归
• 第三次递归处理4，将字符串改变成"5"后继续递归
• 第四次递归处理5，将字符串改变成""后继续递归
• 最后发现字符串为空了，将结果放到列表中并返回
• 上面是从函数调用的角度去看的，而每次调用下一层递归时，都需要将本层的一些处理结果放到一个临时变量中，再传递给下一层，从这个变量层层传递的变化看，就像一棵树一样，这个算法的时间复杂度很高，是O(3^n)这个级别的，空间复杂度是O(n)

​

👻方法1：回溯

​ 核心：解决快速寻找数组中所有存在目标字母的方法: Map加回溯（深度优先搜索思路）

/**
 * 17.电话号码的字母组合
 */
public class Solution {

    // 定义Map哈希表存储数字和对应字母
    Map<Character, String> phoneMap = new HashMap<Character,String>() {{
        put('2', "abc");
        put('3', "def");
        put('4', "ghi");
        put('5', "jkl");
        put('6', "mno");
        put('7', "pqrs");
        put('8', "tuv");
        put('9', "wxyz");
    }};

    // 定义结果集和临时存储的结果字符串
    List<String> res = new ArrayList<>();
    StringBuffer buffer = new StringBuffer();

    // 定义回溯方法
    public void backtrack(String digits, int index) {
        if (index == digits.length()) { // 如果处理完所有的数字，则将当前的字母组合加入到结果集合中
            res.add(buffer.toString()); // 添加满足的序列
        }
        else {
            // 获取当前数字对应的字母序列
            char digit = digits.charAt(index);
            String letters = phoneMap.get(digit);
            // 遍历所有字母，对每一个字母，递归找出剩余数字的所有字母组合
            for (int i = 0; i < letters.length(); i++) {
                buffer.append(letters.charAt(i)); // 将当前字母添加到当前的字母组合中
                backtrack( digits, index+1);// 递归找出剩余数字的所有字母组合
                buffer.deleteCharAt(index);// 回溯，删除当前字母，便于尝试下一个字母
            }
        }
    }

    public List<String> letterCombinations(String digits) {
        // 判断数组是否为空,数组为空直接返回空结果集
        if(digits.isEmpty()) {
            return res;
        }
        // 数组不为空，执行回溯
        backtrack(digits, 0);
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法2：队列法

​ 结合思路分析，其本质就是依次遍历每一个数字，然后构建相应的序列，可以采用队列的方式执行（这种解法思路有点类似【子集】的动态规划解法）。以"23"为例分析队列的执行思路：

• 23对应的字母序列分别为abc、def

• 初始化结果集为[""]（里面只有一个空字符串作为起始）

• 遍历到第1个元素【数字2】：计算队列长度，依次取出队列元素，随后将当前字符串拼接成新字符串进行入队

  • 取出""空字符串，然后将其与数字2对应的字符a、b、c分别拼接为3个字符串进行依次入队
  • 入队完成，此时队列中有"a"、"b"、"c"三个字符串

• 遍历到第2个元素【数字3】：计算队列长度，依次取出队列元素，随后将当前字符串拼接成新字符串进行入队

  • 先取出"a"字符串，然后将其与数字3对应的字符d、e、f分别拼接为3个字符串进行依次入队 => "ad"、"ae"、"af"入队
  • 类似地，取出"b"字符串，随后"bd"、"be"、"bf"入队
  • 类似地，取出"c"字符串，随后"cd"、"ce"、"cf"入队

• 以此类推，直到遍历完所有的数字，最终前面的内容都会出队，而最终保留的是多种组合拼接后的字符序列

/**
 * 17.电话号码的字母组合
 * 思路：队列法
 */
public class Solution2 {

    // 定义Map哈希表存储数字和对应字母
    Map<Character, String> phoneMap = new HashMap<Character, String>() {{
        put('2', "abc");
        put('3', "def");
        put('4', "ghi");
        put('5', "jkl");
        put('6', "mno");
        put('7', "pqrs");
        put('8', "tuv");
        put('9', "wxyz");
    }};

    public List<String> letterCombinations(String digits) {
        // 如果digits为空直接返回空字符串
        if(digits == null || digits.length() == 0){
            return new ArrayList<>();
        }

        // digits 不为空
        List<String> res = new ArrayList<>();
        res.add(""); // 初始化空字符串入队
        for (int i = 0; i < digits.length(); i++) {
            // 获取当前元素及对应的字母序列
            String letters = phoneMap.get(digits.charAt(i));
            // 获取当前集合的大小（集合大小在后续循环操作过程中入队会变化，此处先记录当次循环结果集的大小）
            int resSize = res.size();
            // 将对应字母依次入队（在原有结果集基础上进行拼接）
            for (int j = 0; j < resSize; j++) {
                String s = res.remove(0); // 取出队首元素，然后依次和对应的字母序列进行拼接并将产生的结果入队
                for (int k = 0; k < letters.length(); k++) {
                    res.add(s+letters.charAt(k));
                }
            }
        }
        // 返回结果集
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡04-组合总和（39）

1.题目内容

​ 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

​ candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

​ 对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

2.题解思路

👻方法1：递归

​ 一些解法中会将ans和path作为方法入参，是为了避免并发场景问题，此处将其抽离为了更好地理解代码逻辑结构

​ 核心：深度遍历得到相应路径，计算路径和是否满足target条件，如果大于则直接剪断，如果等于则满足条件加入结果集，如果小于则继续下一层遍历

public class Solution {

    private List<List<Integer>> ans = new ArrayList<>();
    private List path = new ArrayList<>();
    private int[] candidates;
    private int target;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        this.candidates = candidates;
        this.target = target;
        dfs(0, 0); // 初始化从0开始，sum初始化为0
        return ans;
    }

    // 深度优先遍历思路，查找满足条件的路径
    private void dfs(int start, int sum) {
        // 如果指定和等于目标值，则加入结果集
        if (sum == target) {
            ans.add(new ArrayList<>(path));
            return;
        }
        // 如果指定和大于目标值则剪断
        if (sum > target) {
            return;
        }

        // 如果指定和小于目标值，则继续深度遍历、回溯
        for (int i = start; i < candidates.length; i++) {
            path.add(candidates[i]); // 将当前位置遍历元素加入路径
            dfs(i, sum + candidates[i]); // 深度遍历
            path.remove(path.size() - 1); // 回溯
        }
    }

}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡05-括号生成（22）

1.题目内容

​ 数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

2.题解思路

👻方法1：暴力法

​ 最简单粗暴的方式就是通过递归生成所有的括号序列，然后通过自定义方法校验序列是否有效

public class Solution1 {

    // 定义全局结果集合
    private List<String> res = new ArrayList<String>();

    // 核心：通过递归生成所有的括号序列，随后依次调用自定义方法来校验序列的有效性

    public List<String> generateParenthesis(int n) {
        generate(new StringBuilder(),n);
        return res;
    }

    public void generate(StringBuilder cur,int max) {
        // cur:当前生成的括号字符序列，max最大括号对数

        // 校验字符串长度
        if(cur.length() == 2*max) {
            // 校验括号字符序列的有效性，有效则加入结果集
            if(isValid(cur.toString())){
                res.add(cur.toString());
            }
        }else{
            // 加入左括号或者右括号,然后深度遍历到底部校验序列
            cur.append("("); // 加入左括号
            generate(cur,max);
            cur.deleteCharAt(cur.length()-1); // 复原

            cur.append(")"); // 加入右括号
            generate(cur,max);
            cur.deleteCharAt(cur.length()-1); // 复原
        }
    }

    /**
     * 自定义方法校验括号字符序列的有效性
     * @param str
     * @return
     */
    private boolean isValid(String str) {
        int balance = 0; // 定义平衡参数校验括号字符序列的有效性
        for(char c : str.toCharArray()){
            if(c=='('){
                balance++;
            }else if(c==')'){
                balance--;
            }
            if (balance < 0) {
                return false;
            }
        }
        return balance == 0;
    }

}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法2：回溯

​ 基于深度遍历的思路，结合方法一进行优化，可以根据左括号的个数来决定放右括号，递归函数核心分析如下所示

• 递归出口：如果当括号字符串长度等于2*max说明符合条件接入结果集
• 如果左括号<max，说明还可以继续放左括号，基于此进行放入左括号、递归、回溯
• 如果右括号<左括号，说明需要补足右括号，基于此放入右括号，递归、回溯

/**
 * 22.括号生成
 */
public class Solution {

    // 定义全局结果集合
    private List<String> res = new ArrayList<String>();

    public List<String> generateParenthesis(int n) {
        backtrack(0,0,n,new StringBuilder());
        return res;
    }

    // 思路：回溯法（深度遍历，根据左括号来决定放右括号）
    public void backtrack(int left, int right, int max, StringBuilder cur) {
        // left:左括号个数、right：右括号个数、max最大括号对数、cur当前构建的字符串序列

        // 如果当前括号字符串序列长度=2*max，说明符合条件（左右匹配规则在后面进行限定、剪枝，如果到达叶子节点则说明是满足的序列）
        if (cur.length() == 2 * max) {
            res.add(cur.toString());
            return;
        }

        // 如果左括号个数不足max说明还可继续添加左括号
        if (left < max) {
            cur.append("("); // 添加左括号
            backtrack(left + 1, right, max, cur); // 递归
            cur.deleteCharAt(cur.length() - 1); // 回溯
        }

        // 如果右括号小于左括号说明需要补足右括号
        if (right < left) {
            cur.append(")");
            backtrack(left, right + 1, max, cur);// 递归
            cur.deleteCharAt(cur.length() - 1); // 回溯
        }
    }

}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡06-单词搜索（79）

1.题目内容

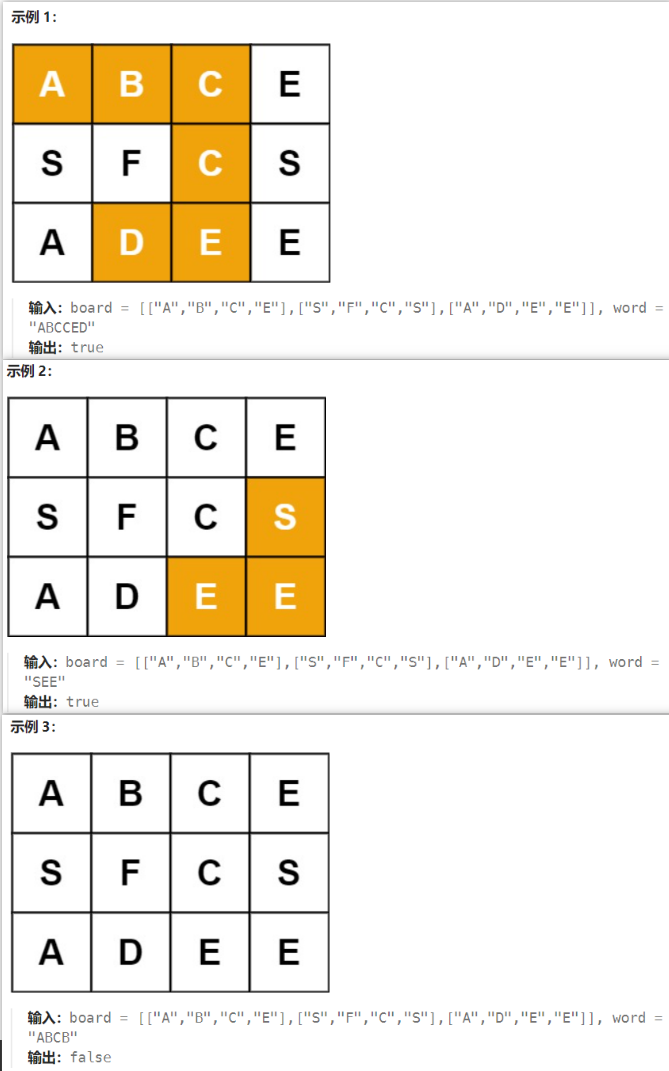
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用

2.题解思路

👻方法1：回溯

​ 核心：循环遍历一个二维数组元素，由其为起点出发进行dfs操作，校验结果即可

• 终止条件：
  • 如果遇到边界、当前矩阵元素和目标字符不符、当前矩阵元素已经被访问过这几种情况则返回false
  • 如果遍历到目标字符串的最后一位则说明全部匹配，返回true
• 递推工作：
  • 将当前矩阵元素标记为已访问（例如'/0'）
  • 随后四个方向执行dfs操作（搜索下一单元格，向四个方向进行检索），如果四个方向中存在一个满足条件则直接返回（或操作，不需要全部找出）
  • 还原矩阵元素（将矩阵元素复原至原来的值）

/**
 * 79.单词搜索
 */
public class Solution {
    public boolean exist(char[][] board, String word) {
        // 调用递推方法实现检索：依次遍历二维数组每个元素
        int m = board.length;
        int n = board[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 调用递归方法校验是否存在路径，如果存在则直接记录结果返回
                if (dfs(board, word, 0, i, j)) {
                    return true;
                }
            }
        }
        return false;
    }


    /**
     * dfs检索
     */
    public boolean dfs(char[][] board, String word, int idx, int row, int col) {
        // 结束条件（遇到边界（索引为负数或者超出长度）、当前元素与目标元素不符、当前元素已被访问则返回false；如果遍历到word的最后一位则说明存在匹配word则返回true）
        // 返回false的情况
        if (row >= board.length || row < 0 || col >= board[row].length || col < 0 || board[row][col] != word.charAt(idx) || board[row][col] == '0') {
            return false;
        }
        // 返回true的情况
        if (idx == word.length() - 1) {
            return true;
        }
        // 进入递推（将元素进行标记，随后往四个方向进行递推，最终复原元素）
        char ch = board[row][col]; // 记录当前遍历元素，并标记为已访问
        board[row][col] = '0';
        if (dfs(board, word, idx + 1, row - 1, col) || dfs(board, word, idx + 1, row + 1, col) || dfs(board, word, idx + 1, row, col - 1) || dfs(board, word, idx + 1, row, col + 1)) {
            return true; // 如果四个方向中有满足条件的则返回true
        }
        board[row][col] = ch; // 复原现场
        return false;
    }
}

• 复杂度分析

  • 时间复杂度：最坏情况下需要遍历字符串长度为K的所有方案，时间复杂度为O（3^KMN）（一共有M×N个起点，每个起点对应方案数为3^K（dfs搜索中有4个方向可以选择，舍弃回头的上个字符的方向，剩下3种选择））

  • 空间复杂度：O(K) 递归深度不超过K，因此系统累计使用的栈空间占用为O(K)（因为函数返回之后，对应的栈空间也会释放），最坏情况下K=MN（递归深度为MN，即所有节点都走一遍）

🟡07-分割回文串（131）

1.题目内容

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

2.题解思路

👻方法1：

​ 核心：求分割子集、判断回文，当分割的指针走到最后一个元素则将当前结果加入结果集

/**
 * 131.分割回文串
 */
public class Solution {

    // 定义结果集
    List<List<String>> res = new ArrayList<List<String>>();
    // 定义临时子集
    List<String> temp = new ArrayList<>();

    /**
     * 核心：求子集、判断回文
     *
     * @param s
     * @return
     */
    public List<List<String>> partition(String s) {
        dfs(0, s); // 执行dfs操作，起始从0开始
        return res; // 返回结果
    }

    /**
     * 构造递推方法（深度遍历）
     * idx 为当前切割位置，s为目标字符串
     */
    public void dfs(int idx, String s) {
        // 如果切割位置和字符串长度相同，则更新结果集并返回
        if (idx == s.length()) {
            res.add(new ArrayList<>(temp)); // 此处需设定new一个子集
            return;
        }
        for (int i = idx; i < s.length(); i++) {
            // 判断是否为回文字符串
            String subStr = s.substring(idx, i + 1);
            if (isHuiWen(subStr)) {
                // 加入回文字符串，然后进行递推操作，最后复原现场
                temp.add(subStr); // 加入子集
                dfs(i + 1, s); // 执行递推
                temp.remove(temp.size() - 1); // 复原现场
            }
        }
    }

    // 双指针校验回文：校验效率较高（参考整体响应8ms）
    public boolean isHuiWen1(String str) {
        // 通过双指针来校验回文，指针相遇则说明满足回文
        int start = 0;
        int end = str.length() - 1;
        while (start < end) {
            if (str.charAt(start) != str.charAt(end)) {
                return false;
            }
            // 指针移动
            start++;
            end--;
        }
        return true;
    }

    // 字符串反转校验回文，校验效率较低（参考整体响应16ms）
    public boolean isHuiWen(String str) {
        // 通过字符串反转来校验回文
        String reverseStr = new StringBuilder(str).reverse().toString();
        return str.equals(reverseStr);
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

// 参考简单写法
class Solution {
    List<List<String>> ans = new ArrayList<List<String>>();
    List<String> temp = new ArrayList<String>();
    public List<List<String>> partition(String s) {
        dfs(s,0);
        return ans;
    }
    public void dfs(String s,int index){
        if(index == s.length()){
           ans.add(new ArrayList<String>(temp));
        }
        for(int i = index;i < s.length();i++){
            String str = s.substring(index,i+1);
            String reversedStr = new StringBuilder(str).reverse().toString();
            if(reversedStr.equals(str)){
                temp.add(str);
                dfs(s,i+1);
                temp.remove(temp.size()-1);
            }
        }
        
    }
}

🔴08-N皇后（51）

1.题目内容

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位

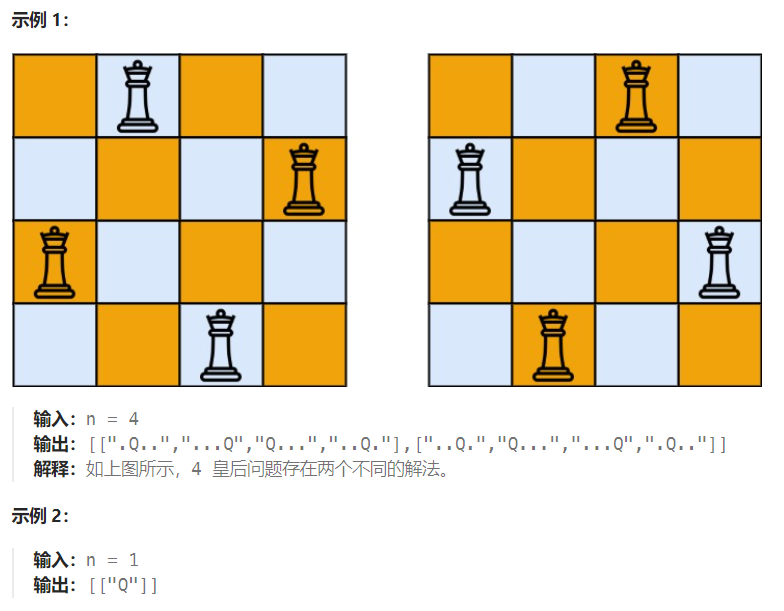
2.题解思路

👻方法1：

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡01-全排列（46）

1.题目内容

2.题解思路

👻方法1：

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：