难度说明：🟢简单🟡中等🔴困难

栈

🟢01-有效的括号（20）

1.题目内容

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合
2. 左括号必须以正确的顺序闭合
3. 每个右括号都有一个对应的相同类型的左括号

2.题解思路

👻方法1：栈（借助栈作为辅助结构，左括号入栈）

​ 需注意此处使用栈的思路是因为题目所需的数据结构符合栈的特性（先进后出），将对应的左括号进行压栈，如果遍历过程中发现当前字符和出栈的括号匹配则视为满足条件，一旦出现不匹配或者最终栈中残余元素，则说明这个字符串括号无效

​ 结合题意说明，此处一堆括号是可以包含另一对括号的，但是不能"交替出现"，例如[{}]是有效的，而[{]}是无效的，因此此处可用栈来确保顺序

​ 核心实现思路说明如下：遍历字符串序列，如果是左括号入栈，右括号则校验栈顶元素是否和其匹配

• 循环遍历字符串的每个字符，校验其是否符合括号定义，进而决定出入栈操作（整个过程只有左括号入栈）
  • 此处为了提升检索效率，将每对括号以哈希表的方式存储，Map<右括号,左括号>
  • 入栈：如果非匹配字符，则执行入栈操作
  • 出栈：如果是匹配的右括号，则执行出栈操作，校验括号是否成对
• 最终通过校验遍历结束后stack是否为空来判断字符串是否有效

public boolean isValid(String s) {
    // 定义Map存储成对的括号映射(Map<右括号,左括号>)
    Map<Character, Character> map = new HashMap<Character, Character>();
    map.put(')','(');
    map.put('}','{');
    map.put(']','[');
    // 定义栈进行辅助
    Stack<Character> stack = new Stack<Character>();
    // 循环遍历字符串进行校验（如果不在key集合中则执行入栈操作（说明是左括号，进行压栈），如果在key集合中则进行出栈并校验括号是否匹配）
    for(char c : s.toCharArray()) {
        if(map.containsKey(c)) {
            // 校验出栈操作(如果栈为空或者校验第一个出栈的括号校验不匹配(确保括号顺序)，则说明字符串无效)
            if(stack.isEmpty() || stack.peek() != map.get(c)) { // peek()方法 查看栈顶元素而不移除
                return false;
            }
            // 执行出栈操作
            stack.pop(); // pop方法移除并返回栈顶元素
        }else{
            // 非右括号（左括号入栈）
            stack.push(c);
        }
    }
    // 校验最终stack中的元素，如果还存在元素则说明不匹配
    return stack.isEmpty();
}

// 优化点1：此处map的设计是一种优化方向，如果不用map则正常用这个思路结合条件语句去做即可
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack=new Stack<>();
        for(int i=0;i<s.length();i++){
            char c=s.charAt(i);
            if(c=='('||c=='['||c=='{'){stack.push(c);}
            else if(stack.isEmpty()||c==')'&&stack.pop()!='('||c==']'&&stack.pop()!='['||c=='}'&&stack.pop()!='{'){return false;}
        }
        return stack.isEmpty();
    }
}

// 优化点2：可以预先判断字符串长度是否为偶数，如果不为偶数则括号肯定不匹配，就没有遍历的必要了，这也是一个优化方向
if(s.lenght()%2!=0){
    return false;
}

• 复杂度分析
  • 时间复杂度：
  • 空间复杂度：

👻方法2：规律法

​ 既然括号不能嵌套出现，那么只需要依次去除成对的括号，看最终是否剩余元素。由于并不知道哪些括号包含其他括号，因此每次去除都直接覆盖所有情况，去掉成对的括号，然后校验剩余的括号是否可以组成成对的括号进行移除（即每次遍历都校验是否有成对的括号直接去除，然后产生的新字符串再次进行校验去除成对括号，以此类推）

// 思路：替换法
public boolean isValid02(String s) {
    /**
         * 既然括号不能嵌套出现，那么只需要依次去除成对的括号，看最终是否剩余元素
         * 由于并不知道哪些括号包含其他括号，因此每次去除都直接覆盖所有情况，去掉成对的括号，然后校验剩余的括号是否可以组成成对的括号进行移除
         * 以此类推
          */

    while(s.contains("[]")||s.contains("{}")||s.contains("()")){
        s = s.replace("[]","");
        s = s.replace("{}","");
        s = s.replace("()","");
    }
    // 最终返回空字符串则说明字符串有效
    return s.equals("");
}


// 参考
func isValid(s string) bool {
    // 判断当前串是否包含成对的括号 直至没有
    for strings.Contains(s, "()") ||
        strings.Contains(s, "[]") ||
        strings.Contains(s, "{}") {
        // 把成对的括号替换为空串，即把成对的括号消去
        // 例如本次替换："(([]){})" => "(())"
        s = strings.Replace(s, "()", "", -1)
            s = strings.Replace(s, "[]", "", -1)
            s = strings.Replace(s, "{}", "", -1)
    }
    // 如果符合要求，最终整个字符串会被替换为空串
    return s == ""
}

• 复杂度分析
  • 时间复杂度：
  • 空间复杂度：

🟡02-最小栈（155）

1.题目内容

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈

实现 MinStack 类:

• MinStack() 初始化堆栈对象
• void push(int val) 将元素val推入堆栈
• void pop() 删除堆栈顶部的元素
• int top() 获取堆栈顶部的元素
• int getMin() 获取堆栈中的最小元素

2.题解思路

👻方法1：辅助栈

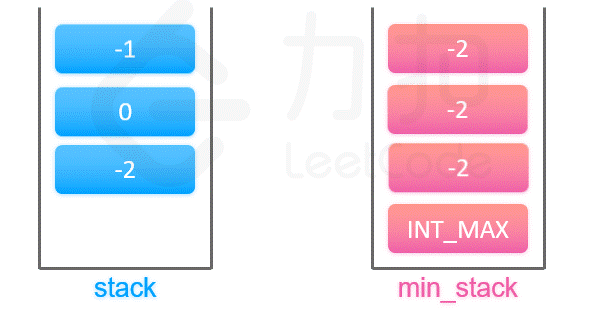
​ 辅助栈思路：相当于每次维护两个栈内容，一个是普通的stack记录正常的栈内容，一个是minStack记录的是同步操作stack对应时刻栈元素的最小值，在入栈和出栈的时候同步维护这两个栈即可。

​ 如果一开始按照单个栈的思路实现，可能会有点懵，因为要确保获取堆栈最小元素的时间复杂度为常数级别，最开始想到的可能是在栈顶去维护这个当前的最小值（例如入栈和出栈操作时同步维护min在栈顶的更新）

class MinStack {

    private Deque<Integer> stack;
    private Deque<Integer> minStack;

    // 初始化堆栈对象
    public MinStack() {
        // 初始化
        stack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        // 初始化设置minStack为一个最大值
        minStack.push(Integer.MAX_VALUE);
    }

    // 将元素val推入堆栈
    public void push(int val) {
        // 入栈操作（校验最小值）
        /* 异常
            if(!minStack.isEmpty()) {
                // 同步维护辅助栈minStack
                if(val < minStack.peek()) {
                    minStack.pop(); // val更小，则更新minStack(先弹出栈顶元素，然后将相应的最小值入栈)
                    minStack.push(val);
                }
            }
             */
        minStack.push(Math.min(minStack.peek(), val));
        // 数据正常入栈
        stack.push(val);
    }

    // 删除堆栈顶部的元素
    public void pop() {
        // 出栈则正常同步弹出即可（因为在push的时候同步维护了相应的最小值）
        minStack.pop();
        stack.pop();
    }

    // 获取堆栈顶部的元素
    public int top() {
        // 返回栈顶元素
        return stack.peek();
    }

    // 获取堆栈中的最小元素
    public int getMin() {
        // 从辅助栈中同步获取
        return minStack.peek();
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡03-字符串解码（394）

1.题目内容

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入

示例 1：
输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：
输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：
输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

示例 4：
输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"

2.题解思路

❌方法1：依次将字母、[、数字入栈，遇到 ] 则出栈处理序列

​ 不足：处理嵌套的情况有待考察

​ 核心：以3[a]2[bc]为例，相当于依次将一组数据入栈3[a当遇到]时候，此时stack中是一组待处理的数据，则以[为分割，分别得到数字、重复序列，然后更新字符串

​ 但是对于嵌套的形式3[a2[c]]则需另外优化存储结构和处理策略

// 不足：对于嵌套的情况，这种思路还需进一步完善，无法处理嵌套的场景
// 栈思路：数字、[、字母依次进栈（这是一组待repeat的数据，以[进行分割），遇到]则出栈
public String decodeString(String s) {
    // 定义辅助栈存储数据
    Deque stack = new LinkedList();
    // 定义当前重复的字符串值和个数
    StringBuffer curNum = new StringBuffer();
    StringBuffer curString = new StringBuffer();
    // 定义结果
    StringBuffer res = new StringBuffer();
    // 遍历字符串
    for (char c : s.toCharArray()) {
        // 如果是数字、[、字母依次入栈
        if (c > '0' && c <= '9') {
            stack.push(c);
        } else if (Character.isLetter(c)) { // c>'a'&&c<'z'
            stack.push(c);
        } else if (c == '[') {
            stack.push('[');
        } else if (c == ']') {
            // 依次出栈，处理数据
            while (!"[".equals(String.valueOf(stack.peek()))) { // 此处需要将对象转化为字符串进行比较处理
                System.out.println("[".equals(stack.peek()));
                System.out.println("cur c:" + stack.peek());
                // 字符依次出栈
                curString.append(stack.pop()); // 此处出栈产生的字符出对比原有是逆序的
            }
            // "[" 字符出栈
            stack.pop();
            // 数字出栈（直到遇到非数字）
            while (stack.peek() != null && (Character) stack.peek() > '0' && (Character) stack.peek() < '9') {// while(!stack.isEmpty()) 需注意嵌套的情况
                // 数字依次出栈
                curNum.append(stack.pop());
            }
            // 处理重复序列，更新序列结果（需将数字和字符串进行反转，获取正确的值）
            res.append(genStr(Integer.valueOf(reverseString(curNum.toString())), reverseString(curString.toString())));
            // 重置临时值
            curNum = new StringBuffer();
            curString = new StringBuffer();
        }
    }

    // 返回最终结果
    return res.toString();
}

// 反转序列
public String reverseString(String s) {
    StringBuffer sb = new StringBuffer();
    for (int i = s.length() - 1; i >= 0; i--) {
        sb.append(s.charAt(i));
    }
    return sb.toString();
}

// 根据重复次数和字符串生成字符序列
public String genStr(int num, String s) {
    StringBuffer newStr = new StringBuffer();
    for (int i = 0; i < num; i++) {
        newStr.append(s);
    }
    return newStr.toString();
}

public static void main(String[] args) {
    String s = "3[a]2[bc]";
    Solution solution = new Solution();
    System.out.println(solution.decodeString(s));
}

👻方法2：栈思路

​ 类似的，实际上对于嵌套的处理是要将最里面的括号一步步向上转化成字符串序列，因此在迭代的过程中要处理这块嵌套的内容（而不是像上面的方法这样，简单根据]划分组合进行处理），可以结合例子理解其在栈的中存取应用。例如此处以3[a2[c]]为例，其拆解思路如果按照上述的代码是无法处理这种嵌套情况的，因此先从理论分析其如何演变，然后再结合代码理解：

3[a2[c]]=>3[acc]（将两个c解析出来组成新的字符串）=>accaccacc（进一步解析外层的括号）

​ 类似的，以ab3[cd2[ab]]2[bc]为例，其解析思路分析如下：

​ 但实际上从代码实现的角度上来说并不可能一步到位就能立刻定位到最内部的[]元素，而是从左往右一步步进行匹配得到结果。因此可以结合思路1中的拆解思路，尝试着从存储和处理上进行调整，从解析思路分析整个过程是后处理的字符串要先使用，因此使用栈结构实现。以ab3[cd2[ab]]2[bc]为例（实际为1[ab]3[cd2[ab]]2[bc]为例），可以定义一个Map结构作为栈元素（Map<重复次数num,重复序列>）：

• 初始化(1,"")
• 【步骤1】：(1,ab)入栈（将当前要处理的序列1[ab暂存下来，优先处理后面遇到的]，得到新的字符串再拼接到此处进行处理）
  • 此处遇到]实际也是拆了两步，先弹出(1,ab)得到一个ab序列，然后将序列更新得到(1,ab)
• 【步骤2】：(3,cd)入栈（类似地，继续暂存3[cd）
• 【步骤3】：(2,ab)入栈（类似地，继续暂存2[ab）
• 【步骤4】：遇到]，说明此时[]出现了，需要处理重复序列（出栈处理并更新字符序列），此处弹出栈顶元素(2,ab)，得到一个abab重复序列，其应该拼接到步骤2中的序列进行处理，因此此处步骤拆分为两步：
  • 弹出栈顶元素(2,ab)，得到一个abab临时序列
  • 更新当前栈顶元素序列，即将(3,cd)更新为(3,cdabab)
• 【步骤5】：继续遍历，又遇到]。类似地，参考步骤4的处理方式
  • 弹出栈顶元素(3,cdabab)，得到一个cdababcdababcdabab临时序列
  • 更新当前栈顶元素序列，即将(1,ab)更新为(1,abcdababcdababcdabab)
• 【步骤6】：(2,bc)入栈（类似地，继续暂存2[bc）
• 【步骤7】：遇到]，(2,bc)出栈得到bcbc，然后当前栈顶元素为(1,abcdababcdababcdababbcbc)
• 遍历结束，当前存储的栈顶元素即为最终得到的序列

​ 结合上述分析，可以在遍历的过程中针对字符进行相应的处理：此处涉及到的数据结构（Stack<StringBuffer[]>、临时存储nums记录数字（由于字母是直接追加到栈顶元素value中，此处不需要额外引入临时存储））

• 初始化栈顶元素(1,"")
• 如果是数字，则构造Map对应的key，记录nums
• 如果是[，则创建键值对(nums,"")并入栈
• 如果是字符，则追加字符到当前栈顶元素的value子串中（通过stack.peek()[1].append(c)实现）
• 如果是]，弹出栈顶元素构造重复字符串，然后追加到当前栈顶元素的子串中

public class Solution2 {

    public String decodeString(String s) {
        /**
         * - 如果是数字，则构造Map对应的key，记录num
         * - 如果是`[`，则创建键值对`(num,"")`
         * - 如果是字符，则追加字符到当前栈顶元素的value子串中
         * - 如果是`]`，弹出栈顶元素构造重复字符串，然后追加到当前栈顶元素的子串中
         */
        // 定义辅助结构，栈中存储的是键值对信息(此处用StringBuffer[]便于处理，也可以用Map<StringBuffer, StringBuffer>来替代)
        Stack<StringBuffer[]> stack = new Stack<>();
        // 初始化栈顶元素
        stack.push(new StringBuffer[]{new StringBuffer("1"),new StringBuffer("")});
        // 定义临时存储
        StringBuffer nums = new StringBuffer("");
        // 循环遍历字符串系列进行处理
        for(char c : s.toCharArray()) {
            if(Character.isDigit(c)){
                // 如果是数字则构建key
                nums.append(c);
            }else if(Character.isLetter(c)){
                // 追加到栈顶元素(追加字符到栈顶元素的value)
                stack.peek()[1].append(c); // StringBuffer[] curStackTop = stack.peek(); curStackTop[1].append(c);
            }else if(c == '['){
                // 构建键值对并入栈,定义键值对（每个栈元素对应一个(nums,repeatStr),初始化为(nums,"")）
                StringBuffer[] item = new StringBuffer[]{new StringBuffer("".equals(nums.toString())?"1":nums.toString()), new StringBuffer("")};
                stack.push(item);
                // 入栈成功重置临时存储
                nums = new StringBuffer("");
            }else if(c == ']'){
                // 弹出栈顶元素得到一个重复序列，然后将其追加到当前新的栈顶元素中
                StringBuffer[] item = stack.pop();
                // 根据栈元素生成重复序列
                String newStr = genStr(Integer.valueOf(item[0].toString()), item[1].toString());
                // 追加序列到栈顶元素
                stack.peek()[1].append(newStr);
            }
        }
        // 遍历结束，最终得到的栈顶元素就是最终序列
        return stack.peek()[1].toString();
    }


    /**
     * 根据nums，repeatStr生成重复序列
     */
    public String genStr(int nums,String str){
        StringBuffer sb = new StringBuffer();
        for (int i = 0; i < nums; i++) {
            sb.append(str);
        }
        return sb.toString();
    }

    public static void main(String[] args) {
        String s = "3[a]2[bc]";
//        String s = "3[a2[c]]";
        Solution2 solution = new Solution2();
        System.out.println(solution.decodeString(s));
    }

}

// 参考思路：
- 定义临时存储nums、repeatStr 存储当次的内容：遇到数字、字母则分别进行追加记录
- 遇到[ 入栈（分别将nums、repeatStr入栈，或者参考上述思路构建一个(nums,repeatStr)关系），入栈完成需重置临时存储
- 遇到] 出栈（参考选取的方式进行出栈处理，弹出栈顶元素生成相应的重复序列之后，需要相应追加对应的位置作为下一次重复的参考）
public String decodeString(String s) {
    Deque<String> dq = new LinkedList();
    int num = 0;
    StringBuilder sb = new StringBuilder();
    for(char c : s.toCharArray()){
        if(c>='0' && c<='9'){
            num = num*10+c-'0';
        } else if(c>='a' && c<='z'){
            sb.append(c);
        } else if(c == '['){
            dq.push(sb.toString());
            dq.push(String.valueOf(num));
            sb = new StringBuilder();
            num = 0;
        } else if(c == ']'){
            int popNum = Integer.valueOf(dq.pop());
            StringBuilder sub = new StringBuilder(dq.pop());
            for(int i=0; i<popNum; i++){
                sub.append(sb);
            }
            sb = sub;
        }
    }
    return sb.toString();
}

🟡04-每日温度（739）

1.题目内容

​ 给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]

2.题解思路

❌方法1：暴力循环（超出时间限制）

​ 将题意转化为，比较当前元素与其后所有元素，看后面比它大的下一个元素出现在哪个位置，因此可以采用双重循环+计数的方式实现

// 思路：暴力双层循环+计数
public int[] dailyTemperatures(int[] temperatures) {
    int[] res = new int[temperatures.length];
    // 循环数组元素，看后面比它大的下一个元素出现在哪个位置
    for(int i = 0; i < temperatures.length; i++){
        for(int j = i+1; j < temperatures.length; j++){
            if(temperatures[j] > temperatures[i]){
                res[i] = j-i;
                // 找到第一个比它高的气温即可退出当前循环
                break;
            }
        }
    }
    // 返回结果
    return res;
}

• 复杂度分析

  • 时间复杂度：O(n²)

  • 空间复杂度：O(n)只需要额外的结果数组存储

👻思路2：单调栈

​ 找任一位置左边离它最近的比它大(小)的，右边离它最近的比它大(小)的。就可以考虑用单调栈，每个元素最多压入一次弹出一次，时间复杂度O(N)

​ 正向遍历温度数组，对于每个元素进行判断处理：引入递减栈，栈中存储的是下标索引

• 如果栈为空，则直接将元素入栈
• 如果栈不为空，则需不断比较栈顶元素top和当前指向元素cur
  • 如果cur>top不能直接入栈（因为此处是递减栈），需要不断将栈顶元素弹出直到满足条件，然后再将当前元素索引入栈，并更新结果集
  • 如果cur<top直接入栈

// 思路：单调递减栈
public int[] dailyTemperatures(int[] temperatures) {
    int[] res = new int[temperatures.length];

    // 定义辅助单调递减栈
    Stack<Integer> stack = new Stack<Integer>();

    // 循环数组元素，看后面比它大的下一个元素出现在哪个位置
    for(int i = 0; i < temperatures.length; i++){
        while(!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]){
            // 当出现比当前栈顶元素要大的元素(top<cur)则需将top弹出,直到不满足条件，并将cur索引入栈，更新res
            int preIndex = stack.pop();
            res[preIndex] = i - preIndex;
        }
        // 如果栈为空或者栈顶元素指向索引位置比当前元素小则直接将元素索引入栈
        stack.push(i);
    }
    // 返回结果
    return res;
}

• 以[73,74,75,71,69,72,76,73]案例进行分析，分析每次遍历后的数据更新情况

• i=0：【73】，此时stack为空，直接加入（加入的是索引）

  • stack：【0(73)】
  • res：【0，0，0，0，0，0，0，0】

• i=1：【74】，依次比较栈顶元素，直到找到满足递减条件的元素进行入栈，否则不断弹出栈顶元素并更新res

  • stack：【1(74)】
  • res：【1，0，0，0，0，0，0，0】（索引差值即为元素弹出个数，即相差多少找到第一个比上一个元素大的值）

• i=2：【75】，依次比较栈顶元素，直到找到满足递减条件的元素进行入栈，否则不断弹出栈顶元素并更新res

  • stack：【2(75)】
  • res：【1，1，0，0，0，0，0，0】

• i=3：【71】，比top小可以直接进栈

  • stack：【2(75)，3(71)】
  • res：【1，1，0，0，0，0，0，0】

• i=4：【69】，比top（71）小可以直接进栈

  • stack：【2(75)，3(71)，4(69)】
  • res：【1，1，0，0，0，0，0，0】

• i=5：【72】

  • 比top（69）大：top 出栈，更新res
    • stack：【2(75)，3(71)】
    • res：【1，1，0，0，1（5-4），0，0，0】
  • 继续比较，比top（71）大：top 出栈，更新res
    • stack：【2(75)】
    • res：【1，1，0，2（5-3），1，0，0，0】
  • 继续比较，比top（75）小：满足单调递减，直接入栈
    • stack：【2(75)，5(72)】
    • res：【1，1，0，2，1，0，0，0】

• i=6：【76】

  • 比top（72）大：top 出栈，更新res
    • stack：【2(75)】
    • res：【1，1，0，2，1，1（6-5），0，0】
  • 继续比较，比top（75）大：top 出栈，更新res
    • stack：【】
    • res：【1，1，4（6-2），2，1，1，0，0】
  • 继续比较，stack为空，直接入栈
    • stack：【6(76)】
    • res：【1，1，4，2，1，1，0，0】

• i=7：【73】，比top(76)小，满足单调递减，直接入栈

  • stack：【6(76)，7(73)】
  • res：【1，1，4，2，1，1，0，0】

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：