二分查找
难度说明:🟢简单🟡中等🔴困难
二分查找
🟢01-搜索插入位置(35)
1.题目内容
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法
2.题解思路
查找目标值有多种方式,一般通过遍历集合的形式查找,此处给定了排序数组并且要求时间复杂度为O(log n),因此选用二分查找的思路
👻方法1:二分法
核心:定义start、end两个指针,根据mid所在位置的元素和target进行比较,不断缩小比较区间,最终得到索引位置。如果指定target不存在,则返回该元素应该插入的位置
public int searchInsert(int[] nums, int target) {
// 调用二分法进行检索,如果目标值不存在于数组,则返回将会被按顺序插入的位置
// 定义左右区间指针
int start = 0, end = nums.length - 1;
// 当两个指针相遇循环结束
while(start <= end) {
// 定义中位数指针
int mid = (start + end ) / 2;
if(target == nums[mid]) {
// 如果目标值存在则直接返回
return mid;
}else if(target<nums[mid]) {
// 如果目标在左区间,调整end指针
end = mid - 1;
}else if(target>nums[mid]){
// 如果目标在右区间,调整start指针
start = mid + 1;
}
}
// 如果目标不存在,返回目标按顺序插入的位置(可结合画图理解)
return start;
}
复杂度分析
时间复杂度:
空间复杂度:
🟡02-搜索二维矩阵(74)
1.题目内容
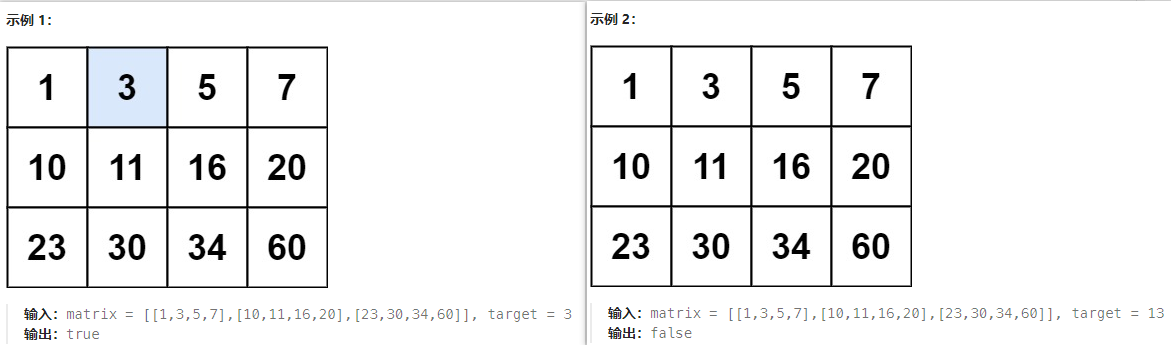
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false
2.题解思路
👻方法1:暴力法
核心:直接双层循环迭代二维数组
// 暴力检索
public boolean searchMatrix(int[][] matrix, int target) {
for(int i = 0; i < matrix.length; i++) {
for(int j=0;j<matrix[i].length;j++) {
if(matrix[i][j] == target) {
return true;
}
}
}
return false;
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:二分查找
方向1:一次二分查找,逐行查找,每一行中使用二分查找进行定位
public boolean searchMatrix(int[][] matrix, int target) { for (int i = 0; i < matrix.length; i++) { // 校验每行的二分检索结果 int findRow = binarySearch(matrix[i],target); // 二分检索成功返回true if (findRow != -1) { return true; } } return false; } /** * 定义二分查找方法(针对一维数组) */ public int binarySearch(int[] row, int target) { int left = 0, right = row.length - 1; while (left <= right) { // 定义中点位置 int mid = left + (right - left) / 2; // 与target进行比较 if(row[mid] == target) { return mid; }else if(target < row[mid]) { right = mid - 1; }else if(target > row[mid]) { left = mid + 1; } } // 无匹配元素返回-1(如果是要返回下一个插入位置则return left或者right+1) return -1; }方向2:扁平化数组然后进行二分查找(即将二维数组转化为有序的一维数组,然后再进行二分查找)
- 这种思路需要额外的一维数组存储空间,将二维数组展开然后直接进行一次二分查找
方向3:坐标转化(类似转一维数组的思路),此处将坐标转换为一维数组下标,然后将题目转为一维数组的二分查找
public boolean searchMatrix(int[][] matrix, int target) { int left = 0, right = (matrix.length * matrix[0].length) - 1; while (left <= right) { int mid = (left + right) / 2; int midX = mid / matrix[0].length; int midY = mid % matrix[0].length; if (matrix[midX][midY] == target) { return true; } else if (matrix[midX][midY] > target) { right = mid - 1; } else { left = mid + 1; } } return false; }复杂度分析
时间复杂度:
空间复杂度:
👻方法3:规律法
左下角的数一定比右上角的数要大。
从左下角开始遍历,如果当前值比 target 小则往右找,如果比 target 大则往上找,如果存在,必然可以找到目标数字。
即选取右上角或者左下角的元素 a[row] [col] 与 target 进行比较, 当target小于元素 a[row] [col] 时,那么 target 必定在元素 a 所在行的左边,让 col– ;当 target 大于元素 a[row] [col] 时,那么 target 必定在元素 a 所在列的下边,让 row++

public class Solution {
public boolean Find(int target, int [][] array) {
int row = 0;
int col = array[0].length - 1;
while(row <= array.length - 1 && col >= 0){
if(target == array[row][col])
return true;
else if(target > array[row][col])
row++ ;
else
col-- ;
}
return false;
}
}
🟡03-在排序数组中查找元素的第一个和最后一个位置(34)
1.题目内容
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
2.题解思路
👻方法1:暴力法
核心:循环遍历数组(数组本身升序排列),定义一个数组存储结果集合,这个结果集可以理解为(第一个匹配的元素索引,第一个匹配的元素索引+匹配个数(作为结束索引))
// 暴力法:循环遍历数组,一次进行校验
public int[] searchRange(int[] nums, int target) {
// 定义结果集(开始索引,结束索引)
int[] res = {-1,-1};
// 定义target在数组中的匹配个数(计数器)
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == target) {
if(count == 0){
// 表示第一个检索到的匹配元素,将其加入结果集
res[0] = i;
}
count++;
}
}
// 最终封装结果集并返回
if(res[0] != -1){
res[1] = res[0] + count -1;
}
return res;
}
还有一种暴力思路就是两头找,从头找第一个符合target的数的索引,从尾找第一个符合target的索引,然后合并结果即可。即正向找一遍进行一次二分搜索,反向找一遍进行二分搜索,然后合并结果,没找到就是-1
复杂度分析
时间复杂度:
空间复杂度:
🟡04-搜索旋转排序数组(33)
1.题目内容
整数数组 nums 按升序排列,数组中的值 互不相同 。
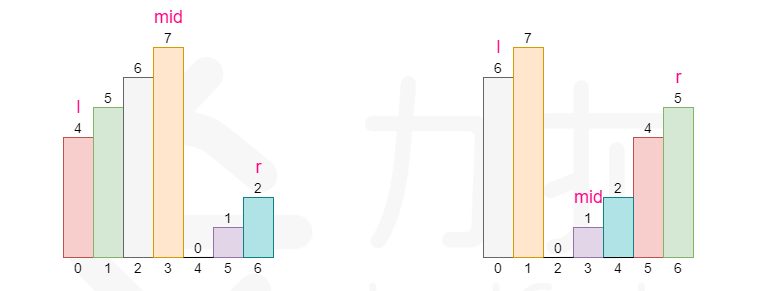
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
2.题解思路
👻方法1:暴力拆分法
既然"旋转"是未知的,那么就要区分有旋转、无旋转两种情况进行分析:
- 如果是无旋转,说明还是原数组,直接通过一次二分法检索即可
- 如果是有旋转,则说明原数组被拆分为两个升序的数组,而这个旋转的轴点是不确定的。那么只需要对这两个升序的数组分别进行二分检索,然后校验结果即可
基于上述分析,就要先确定数组到底有没有旋转,可以通过遍历数组,判断元素是否始终升序(如果突然出现降序,则说明出现旋转,则降序出现的那个位置就是轴点,以此拆分为两个有序数组,然后进行二分检索)
需调试相应数组边界
public int search(int[] nums, int target) {
// 区分有无旋转两种情况,通过判断nums是否完全升序来界定
int validOrderRes = validOrder(nums);
if (validOrderRes == -1) {
// 无旋转,直接进行一次二分检索
return binarySearch(nums, target);
} else {
// 有旋转,基于轴点分别进行二分检索,返回最终检索值(copyOfRange [from,to))
int[] nums1 = Arrays.copyOfRange(nums, 0, validOrderRes+1);
int[] nums2 = Arrays.copyOfRange(nums, validOrderRes+1, nums.length);
int search1 = binarySearch(nums1, target);
int search2 = binarySearch(nums2, target);
if (search1 != -1) {
return search1;
}
if (search2 != -1) {
return search2 + nums1.length; // 返回的是索引,需加上前面的数组长度
}
return -1;
}
}
public int validOrder(int[] nums) {
// 如果数组为空或者数组长度为1,视作无旋转
if (nums == null || nums.length == 0 || nums.length == 1) {
return -1;
}
// 如果完全升序则返回-1,如果非完全升序则返回"轴点"(出现降序的索引位置)
for (int i = 0; i < nums.length -1; i++) {
if (nums[i] > nums[i + 1]) {
return i;
}
}
return -1;
}
/**
* 定义二分检索方法
*/
public int binarySearch(int[] nums, int target) {
// 定义左右节点
int left = 0, right = nums.length - 1;
while (left <= right) {
// 定义中间节点
int mid = left + (right - left) / 2;
// 校验target
if (nums[mid] == target) {
return mid;
} else if (target < nums[mid]) {
right = mid - 1;
} else if (target > nums[mid]) {
left = mid + 1;
}
}
// 无匹配结果
return -1;
}
复杂度分析
时间复杂度:
空间复杂度:
🟡05-寻找旋转排序数组中的最小值(153)
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题
1.题目内容
2.题解思路
👻方法1:暴力法
根据题意,还是拆分旋转和未旋转两个方向:
- 如果未旋转或者旋转次数达到一个轮次(相当于没有旋转),此时nums[0]是最小的
- 如果已旋转,则只需要找到第一个比nums[0] 小的数字,该值一定是最小的(因为旋转后也是两个拆分后的有序数组,如果把它分为前半部分和后半部分,那么nums[0]是作为前半部分的最小值,如果出现比它更小的只能是后半部分的最小值,也就是整个数组的最小值)
public int findMin(int[] nums) {
int low = 0;
int high = nums.length - 1;
while (low < high) {
int pivot = low + (high - low) / 2; // 等价于int pivot = (low + high ) /2;
if (nums[pivot] < nums[high]) { // 因为最小值一定存在,此处只需要不断缩圈
high = pivot;
} else {
low = pivot + 1;
}
}
return nums[low];
}
👻方法2:二分法
类似的,此处将target换成找最小值概念
class Solution {
public int findMin(int[] nums) {
if (nums.length == 0) return -1;
if (nums.length == 1) return nums[0];
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
// 最小值在[mid+1, right]之间
left = mid + 1;
} else if (nums[mid] < nums[right]) {
// 最小值在[left, mid]之间,包括mid
right = mid;
} else {
// 无法确定时,right指针左移一位
right--;
}
}
return nums[left];
}
}
复杂度分析
时间复杂度:
空间复杂度:
