跳至主要內容

链表

holic-x...大约 28 分钟算法算法

难度说明：🟢简单🟡中等🔴困难

链表

🟢01-相交链表（160）

1.题目内容

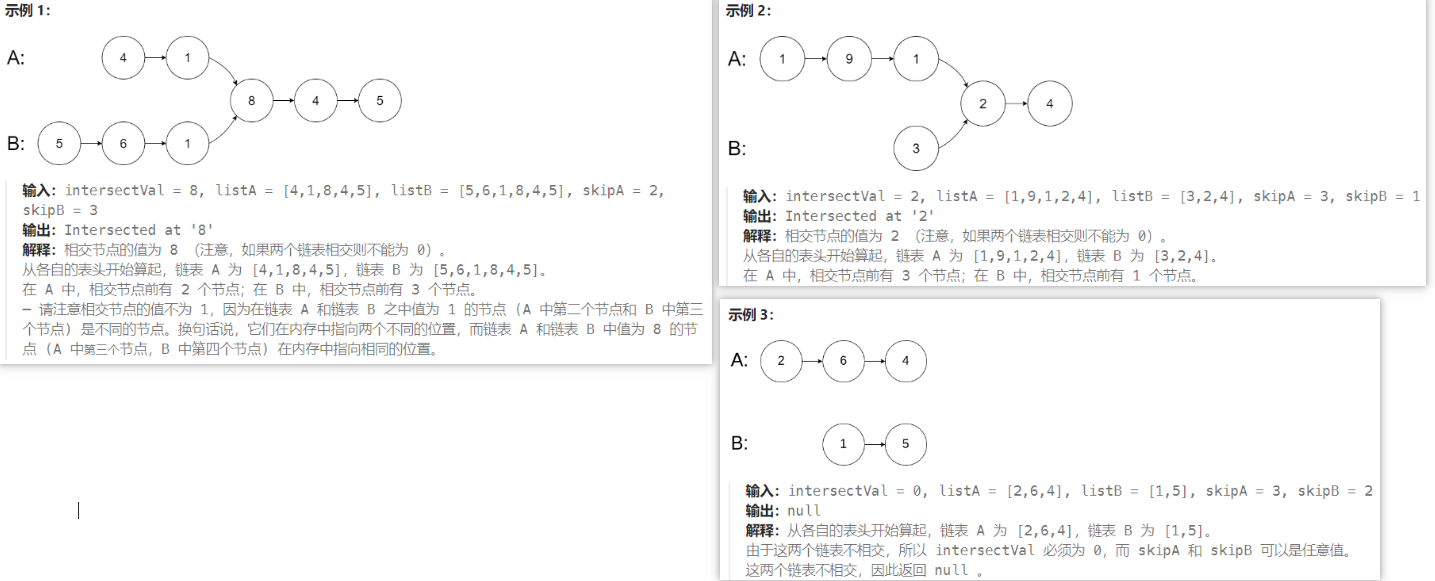
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交

image-20240926075435629

image-20240926075649294

2.题解思路

👻方法1：判断交点

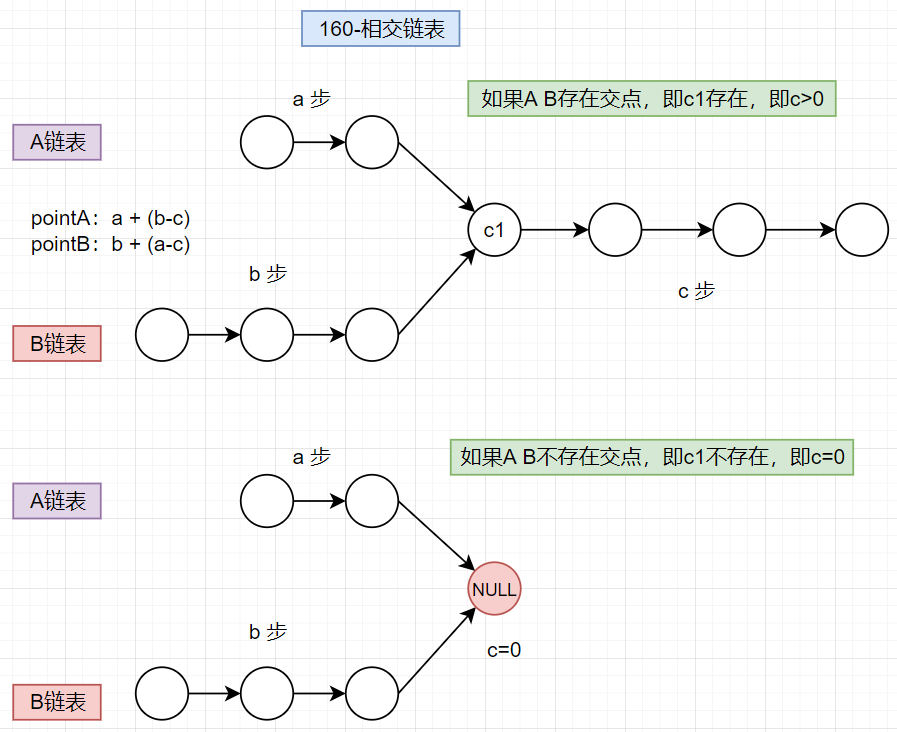
规律分析：无论A、B是否有相交节点，最终都会指向同一个相同的节点（要么是公共尾部、要么是NULL）

  • 初始化：让pointA和pointB分别指向链表A、B的头节点，之后两个指针分别以步幅为1的速度向链表的尾部遍历
  • 当pointA遍历到链表A的尾节点（走了a个节点），然后将pointA指向链表B的头部，继续向后遍历，直到走到c1（即公共尾部），此时指针共走了a+(b-c)步
  • 当pointB遍历到链表B的尾节点（走了b个节点），然后将pointB指向链表A的头部，继续向后遍历，直到走到c1（即公共尾部），此时指针共走了b+(a-c)步

从数学逻辑上分析，a+(b-c)=b+(a-c)是需要成立的：

  • 如果c>0（说明存在公共尾部），即表示c1这个节点是存在的，两链表同时到达c1
  • 如果c=0（说明两链表没有公共尾部），即pointA和pointB都指向NULL

image-20240926081818505

/**
 * 160-相交链表
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode common = null;
        // 判断边界（链表为NULL的情况）
        if (headA == null || headB == null) {
            return null;
        }

        // 初始化指针(pointA、pointB分别指向A、B链表头节点)
        ListNode pointA = headA;
        ListNode pointB = headB;

        // 两个指针指向同一个节点，遍历结束（根据这个共同节点判断是否为null进而确定是否存在公共节点）
        while (pointA != pointB) {
            // 遍历A链表
            if (pointA != null) {
                // 如果pointA不为NULL则不断向后移动
                pointA = pointA.next;
            } else {
                // 如果pointA为NULL则跳到B链表
                pointA = headB;
            }

            // 遍历B链表
            if (pointB != null) {
                // 如果pointB不为NULL则不断向后移动
                pointB = pointB.next;
            } else {
                // 如果pointB为NULL则跳到A链表
                pointB = headA;
            }
        }

        // pointA、pointB最终都指向同一个节点,要么是公共节点、要么是NULL,所以此处返回任意一个都可以
        return pointA;
    }

}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟢02-反转链表（206）

1.题目内容

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表

例如：[1,2,3,4,5] =》[5,4,3,2,1]

2.题解思路

👻方法1：直接颠倒（头插）

​ 思路分析：和数组反转的思路类似，可以直接将值颠倒。数组可以从尾部开始进行遍历，而链表则需从头节点进行遍历。因此此处有一个很巧妙的设定，可以利用头插的思路去实现。定义一个新的链表用于存储结果，依次循环遍历链表元素，将元素取出并插入到链表的最前面（也就是让当前元素的next指针指向当前的res即可，这点可以通过ListNode的构造函数实现）

​ 核心：循环遍历链表元素，将元素以"头插"的形式插入链表

/**
 * 206.反转链表
 * 思路：直接颠倒（头插）
 */
public class Solution1 {
    public ListNode reverseList(ListNode head) {

        // 定义结果
        ListNode res = null;

        // 遍历链表
        for(ListNode cur = head; cur != null; cur = cur.next) {
            // 传入指定值和链表，创建一个ListNode进行初始化，其next指向指定链表（可以理解为头插法的一种体现）
            res = new ListNode(cur.val,res);
        }

        // 返回结果
        return res;
    }
}


/**
 * 链表节点定义
 */
class ListNode {
    int val;
    ListNode next;

    ListNode() {}

    ListNode(int val) {
        this.val = val;
    }

    ListNode(int val, ListNode next) {
        this.val = val;
        this.next = next;
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

👻方法2：栈（先进后出去）

​ 思路分析：链表为【1->2->3->4->5->∅】，需反转为【5->4->3->2->1->∅】，可通过借助栈来实现

​ 核心：循环迭代链表元素，依次入栈，然后依次出栈存入新链表

/**
 * 206.反转链表
 * 思路：栈
 */
public class Solution2 {
    public ListNode reverseList(ListNode head) {

        // 定义结果
        ListNode res = new ListNode(0);
        // 定义当前节点指针
        ListNode cur = res;

        // 定义栈存放中间结果
        Stack<ListNode> stack = new Stack<ListNode>();

        // 遍历链表元素，入栈
        while (head != null) {
            stack.push(head);
            head = head.next;
        }

        // 依次出栈构建新链表
        while(!stack.isEmpty()) {
            cur.next = stack.pop();
            cur = cur.next; // 更新节点
        }
        cur.next = null; // 需设置尾节点为null，否则提示（Error - Found cycle in the ListNode）
        return res.next; // 排除第一个初始化的节点（初始化起始值为0，需从其下一个节点遍历）
    }
}

👻方法3：迭代法

​ 思路分析：链表为【1->2->3->4->5->∅】，需反转为【5->4->3->2->1->∅】，可通过迭代的方式进行

  • 反转的思路是将当前节点的next指针指向其前一个节点
    • 初始化prev、curr（当前节点，理解为节点指针）
    • 迭代元素：记录当前节点的下一个节点，将当前节点的next指针指向prev，然后prev、curr向后移动（即先将当前的curr作为下一个节点的prev，然后curr继续指向下一个节点）
/**
 * 206.反转链表
 * 思路：迭代
 */
public class Solution3 {
    public ListNode reverseList(ListNode head) {

        // 记录当前节点和当前节点的上一个节点
        ListNode prev = null;
        ListNode curr = head;

        // 迭代链表
        while (curr != null) {
            ListNode next = curr.next; // 记录当前节点的下一个节点
            curr.next = prev; // 将当前节点的next指向指向prev
            prev = curr; // prev设定为当前节点（会作为下一节点的prev）
            curr = next; // curr指向下一个节点（继续遍历）
        }

        // 返回链表
        return prev;
    }
}

3.复盘

🟢03-回文链表（234）

1.题目内容

​ 给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false

​ 回文链表：指的是以链表中间为中心点，两边对称。例如[1 2 2 1]

​ 对于回文的判断可以有多个方向切入：

  • 思路1：基于回文概念，可以理解为类似字符串abccba，它正着读和反着读是一样的，因此可以考虑构建一个集合存储它的反转序列，然后对比两个集合对应位置的数值是否匹配（即正转和反转的序列是否一致）
  • 思路2：分割+反转概念，回文序列的前半部分和后半部分是相互对称的，可以先找到中点位置分为前后部分，然后将后半部分进行反转，再与前半部分进行对比确认是否一致

2.题解思路

👻方法1：栈（先进后出）

​ 定义栈存储元素，然后遍历链表和依次出栈的元素进行比较。优化上体现的是，不需要遍历整个集合，可以只遍历一半的元素即可。即在第一次遍历的时候记录链表长度，然后第二次遍历的时候只遍历一半的元素即可

/**
 * 234.回文链表
 * 思路：栈
 */
public class Solution1 {

    public boolean isPalindrome(ListNode head) {

        // 指定stack存储类型
        Stack<Integer> stack = new Stack<>();

        // 记录链表节点指针
        ListNode cur = head;

        // 依次入栈
        while (cur != null) {
            stack.push(cur.val);
            cur = cur.next;
        }

        // 遍历链表，和出栈元素依次进行比较，如果出现不一致则认为非回文
        while (head != null) {
            if (head.val != stack.pop()) {
                return false;
            }
            // 继续指向下一个
            head = head.next;
        }

        // 返回
        return true;
    }

    public static void main(String[] args) {
        ListNode head = new ListNode(1);
        head.next = new ListNode(2);
        Solution1 solution1 = new Solution1();
        System.out.println(solution1.isPalindrome(head));
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：
// 链表逆序打印
private void printListNode(ListNode head) {
    if (head == null)
        return;
    printListNode(head.next);
    System.out.println(head.val);
}

👻方法2：分割

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟢04-环形链表（141）

1.题目内容

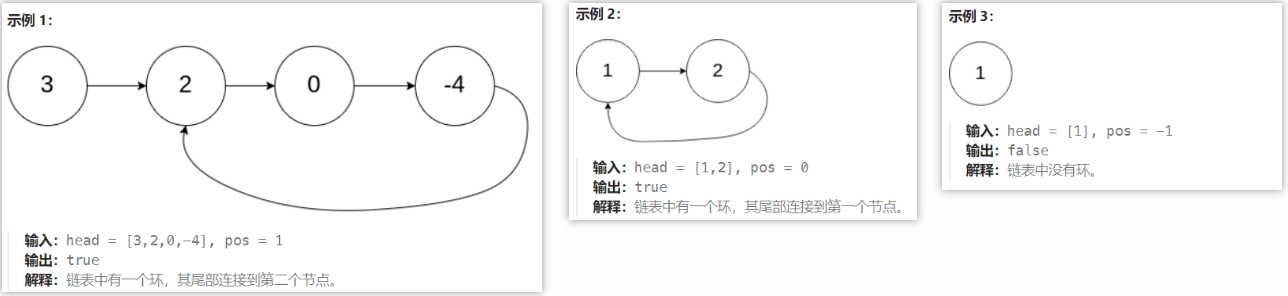
​ 给你一个链表的头节点 head ，判断链表中是否有环。

​ 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

image-20240926111811334

2.题解思路

👻方法1：哈希表

​ 核心：循环遍历链表，然后记录下已访问的元素，如果元素的next节点在已遍历的元素中

/**
 * 141-环形链表
 * 思路：哈希表  迭代、标记，校验next是否已被标记
 */
public class Solution {

    public boolean hasCycle(ListNode head) {

        // 定义HashSet存储元素
        HashSet<ListNode> set = new HashSet<ListNode>();

        // 遍历链表，校验next是否已存在标记
        while(head != null) {
            if(set.contains(head)) {
                return true;
            }
            // 将当前节点进行标记
            set.add(head);
            // 迭代下一个元素
            head = head.next;
        }
        return false;

    }

}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

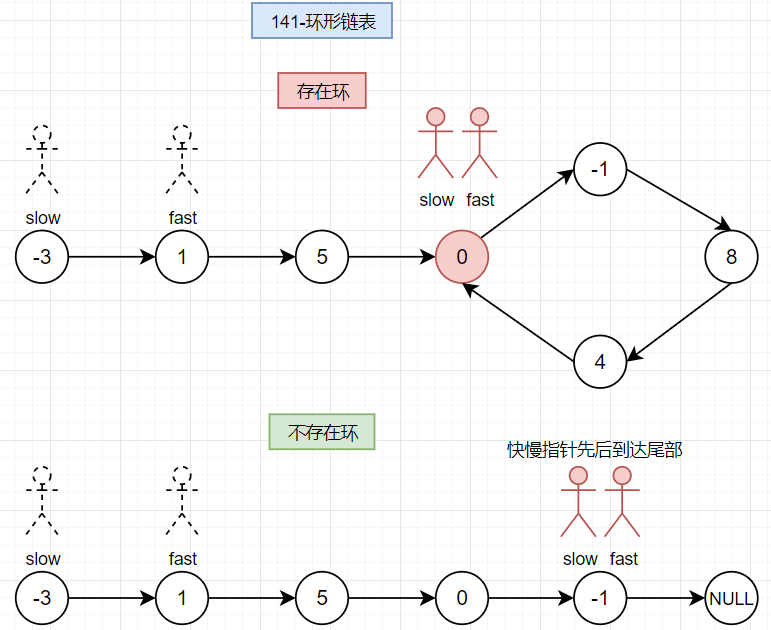
👻方法1：快慢指针

​ 定义快慢指针（fast、slow），只要存在环，则这两个指针必定会在某一时刻相遇

image-20240926134639268

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode s = head, f = head;
        // 如果快指针先走到终点
        while(f != null && f.next != null){ 
            s = s.next; // 慢指针
            f = f.next.next; // 快指针
            if(s == f) return true; // 相遇说明存在环
        }
        return false;
    }
}

3.复盘

🟡05-环形链表II（142）

1.题目内容

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

2.题解思路

👻方法1：哈希表

​ 和141-环形链表题型类似，遍历元素将其加入哈希表，如果遍历过程中发现元素已存在则说明存在环，则直接返回这个节点

/**
 * 142-环形链表II
 * 思路：哈希表  迭代、标记，校验next是否已被标记
 */
public class Solution1 {

    public ListNode detectCycle(ListNode head) {

        // 定义HashSet存储元素
        HashSet<ListNode> set = new HashSet<ListNode>();

        // 遍历链表，校验next是否已存在标记
        while(head != null) {
            if(set.contains(head)) {
                return head;
            }
            // 将当前节点进行标记
            set.add(head);
            // 迭代下一个元素
            head = head.next;
        }
        return null;

    }

}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟢06-合并两个有序链表（21）

1.题目内容

​ 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的

2.题解思路

👻方法1：迭代法

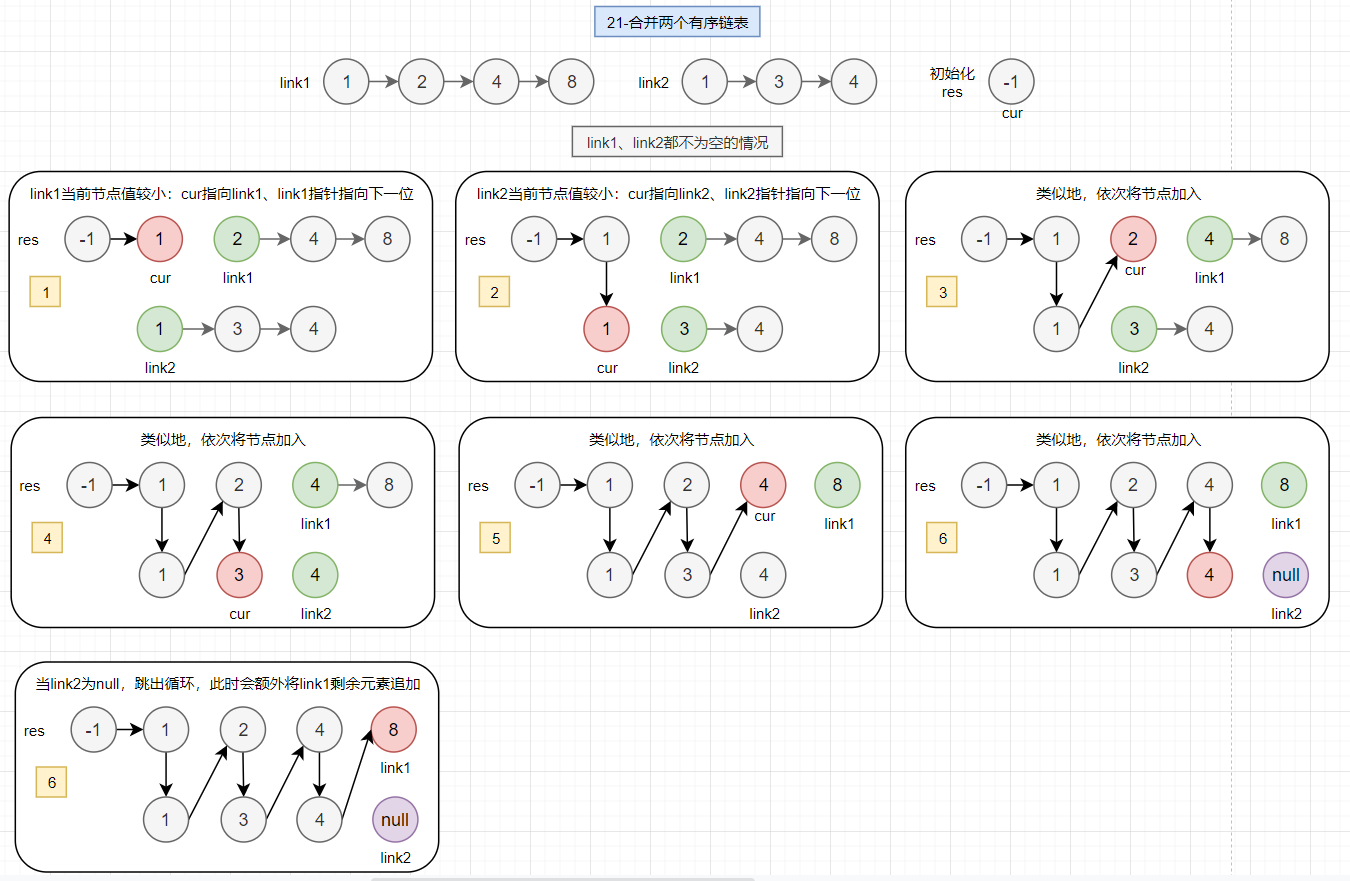
​ 定义一个新链表，然后不断比较两个链表的节点大小，将其依次纳入链表中：

  • 校验边界值：link1、link2为null的情况
  • 当link1、link2都不为null，依次遍历链表，校验对应头节点的值，将较小的节点加入新链表，以此类推
  • 当跳出循环（上述操作遍历到某个链表尾部时就会跳出循环），因此需要将剩余的节点进行追加

image-20240926154012663

/**
 * 21-合并链表
 */
public class Solution1 {

    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {

        // 定义虚拟节点头
        ListNode res = new ListNode(0); // 这个链表头节点可以为任意，因为不需要用到这个头节点的值

        // 定义对应链表指针
        ListNode cur = res;

        // 边界值确认（l1、l2为空的情况）
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }

        // l1、l2都不为空的情况,遍历链表（不断比较l1、l2各个节点的值）
        while (l1 != null && l2 != null) {
            // 如果l1当前节点的值小于l2当前节点
            if (l1.val <= l2.val) {
                cur.next = l1;// 让指针指向当前这个较小的节点链表
                l1 = l1.next; // l1 指向下一个节点（l1向后移动）
            } else {
                cur.next = l2;// 让指针指向当前这个较小的节点链表
                l2 = l2.next; // l2 指向下一个节点（l2向后移动）
            }
            // 指针向后移动
            cur = cur.next;
        }

        // 如果l1、l2还有没有覆盖到的节点（因为不知道l1、l2哪个长，所以上述操作循环结束，可能长的链表中还有节点没有覆盖到）
        if (l1 != null) {
            cur.next = l1; // 将当前l1剩下的节点全部进行追加
        }
        if (l2 != null) {
            cur.next = l2; // 将当前l2剩下的节点全部进行追加
        }
        // 最后返回虚拟节点头的next指针
        return res.next;
    }

}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡07-两数相加（2）

1.题目内容

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头

PS：需注意此处并不是要将每个链表对应位置数字相加，实际上应该要将链表组成的数字进行相加，然后再放在一个新链表中，链表中每个节点存一个数字

例如[2,4,3] [5,6,4]应该为342+465=807需要将807逆序放入链表

2.题解思路

❌方法1：硬核拆解（超出内存限制）

​ 回归题意，最硬核的解法就是分别得到每个链表表示的数字，然后进行相加得到sum，最后将这个sum转化为链表的各个节点。

​ 这个方案虽然硬核，但是非常暴力，使用上会超出内存限制。很明显需要结合题目特性进行优化

/**
 * 2-两数相加
 * 思路：将链表组成的数字相加，然后再放在一个新链表中，链表中每个节点存一个数字）
 */
public class Solution2 {

    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {

        // 定义链表
        ListNode res = new ListNode(0);
        // 定义链表指针
        ListNode cur = res;

        // 分别遍历链表，组合数字
        StringBuffer sb1 = new StringBuffer();
        while(l1!=null){
            sb1.append(l1.val);
        }
        StringBuffer sb2 = new StringBuffer();
        while(l2!=null){
            sb2.append(l2.val);
        }
        // 计算数字之和
        int sum = Integer.valueOf(sb1.toString()) + Integer.valueOf(sb2.toString());

        // 将数字加入链表
        String sumStr = String.valueOf(sum);
        for(int i=0;i<sumStr.length();i++){
            cur.val += sumStr.charAt(i);
            cur = cur.next;
        }
        // 返回链表
        return res.next;
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

👻方法2：节点相加、处理进位

​ 因为数字本身是按照逆序排序的，所以正常按照各个节点相加，然后处理进位关系即可

​ 例如[2,4,3] [5,6,4]，处理为2+5、4+6=10（存0进1）、3+4+1=8（进位），然后将708逆序存入链表，得到807

​ 那么这题的思路就是通过循环遍历得到对应节点之和，然后处理好进位关系即可

​

​ 这点遍历上有点小技巧：

  • 循环条件：因为两个链表可能不等长，因此遍历过程中需要进行NPE处理，如果某个链表为null则其后续所有节点置为0即可。只有当两个链表都遍历完成，才认为遍历结束
  • 最后的进位：由于最后一个节点也可能存在进位，因此最后如果存在进位还需额外补上（或者将进位条件也加入循环，处理好对应的情况即可）
/**
 * 2-两数相加
 * 思路：将各个节点的值进行相加，处理相应的进位关系
 */
public class Solution3 {

    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {

        // 定义链表
        ListNode res = new ListNode(0);

        // 定义链表指针
        ListNode cur = res;

        // 边界值处理（l1为null，或者l2为null）
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }

        // 定义进位标识
        boolean carry = false;
        // 循环遍历两个链表
        while (l1 != null || l2 != null || carry) {
            // 可能会有个链表先为空，需做空指针处理
            int a = l1 == null ? 0 : l1.val;
            int b = l2 == null ? 0 : l2.val;

            // 获取对应节点值之和，需要处理进位关系
            int currentVal = carry ? (a + b + 1) : (a + b); // 如果carry为true需要加上进位
            // 处理当前节点存储数据和进位配置(如果currentVal>=10表示需要进位，当前节点直接存储取模后的数字)
            cur.next = new ListNode(currentVal % 10);
            carry = currentVal >= 10 ? true : false;

            // 指针后移
            cur = cur.next;

            // 判断是否有下一个节点
            if (l1 != null) {
                l1 = l1.next;
            }
            if (l2 != null) {
                l2 = l2.next;
            }
        }

        // 处理最后的进位(也可加进位条件加入循环，而不需此处额外处理)
        /*
        if (carry) {
            cur.next = new ListNode(1);
        }
         */

        // 返回链表结果
        return res.next;
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡08-删除链表倒数的第N个节点（19）

1.题目内容

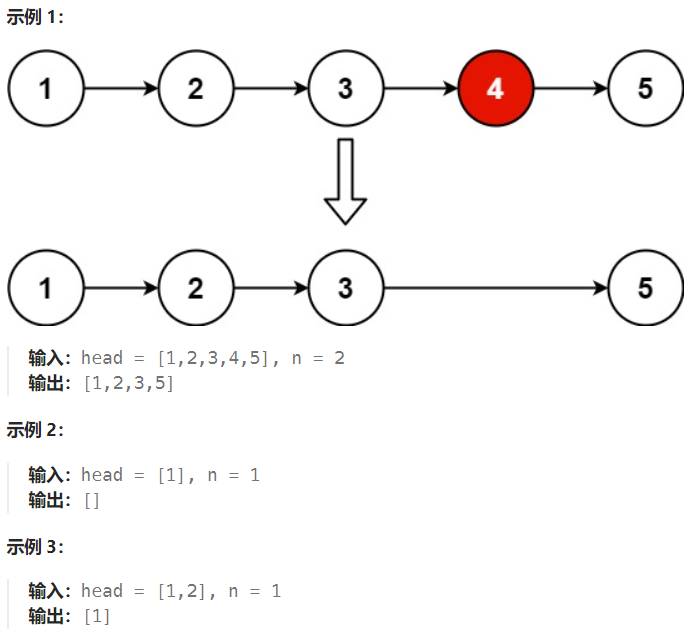
​ 给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

image-20240926172901998

2.题解思路

​ 删除倒数第n个节点，从遍历的角度来看，就是正向遍历链表，然后删除第L-n+1位置的节点。因此需要先计算出链表的长度。这种思路有两种实现方式：

  • 两次遍历链表：第1次遍历得到链表长度L，第2次遍历第L-n+1的位置做删除操作
  • 链表+栈：利用栈的先进后出特性，第1次遍历入栈，第2次遍历出栈（第n个位置做"删除操作"）

核心：需要注意的是，不需要设定为将节点加入新链表，主要是定位到那个要删除的节点的前一个节点prev，然后设置prev.next=prev.next.next

👻方法1：链表遍历

  • 两次链表遍历：（注意遍历的时候用的指针，如果用同一个指针则需要进行重置，否则会干扰）
    • 第1次遍历：计算链表长度
    • 第2次遍历：让指针移动到指定的位置，然后删除对应位置的元素（即让当前指针的next指向next.next）
/**
 * 2-删除倒数第N个节点（链表）
 * 思路1：两次链表遍历，第1次获取链表长度，第2次在对应L-n+1做删除操作（即让当前节点的next指向下下个节点）
 */
public class Solution1 {

    public ListNode removeNthFromEnd(ListNode head, int n) {

        // 定义链表(初始化为原链表)
        ListNode res = new ListNode(0, head);

        // 定义链表指针
        ListNode cur = res;

        // 1.获取链表长度（注意不要用同一个指针）
        int len = 0;
        while (head != null) {
            len++;
            head = head.next;
        }

        // 2.遍历链表,删除第L-N+1个节点(去掉链表初始节点)
        for (int i = 1; i < len - n + 1; i++) {
            cur = cur.next; // 指针移动
        }
        // 当前指针移动向下下个节点（表示删除下个节点）
        cur.next = cur.next.next;
        return res.next;
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

👻方法2：栈

  • 利用栈的先进后出特性
    • 第1次遍历：依次进栈
    • 第2次遍历：依次出栈，排除指定计数N的值
public ListNode removeNthFromEnd(ListNode head, int n) {

        // 定义链表(初始化为head原链表)
        ListNode dummy = new ListNode(0,head);
        // 定义链表指针
        ListNode cur = dummy;

        // 定义栈
        Stack<ListNode> stack = new Stack<ListNode>();

        // 1.依次入栈
        while (head != null) {
            stack.push(head);
            head = head.next; // 指针后移
        }

        // 2.依次出栈，当第n个位置则剔除
        for(int i = 0; i < n; i++) {
            stack.pop();
        }
        // 获取到倒数第n-1的节点，更新其next值即可
        ListNode prev = stack.peek();
        prev.next = prev.next.next;
        return dummy.next;
    }

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡09-两两交换链表中的节点（24）

1.题目内容

​ 给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

image-20240926183728730

2.题解思路

image-20240927103423294

👻方法1：遍历法

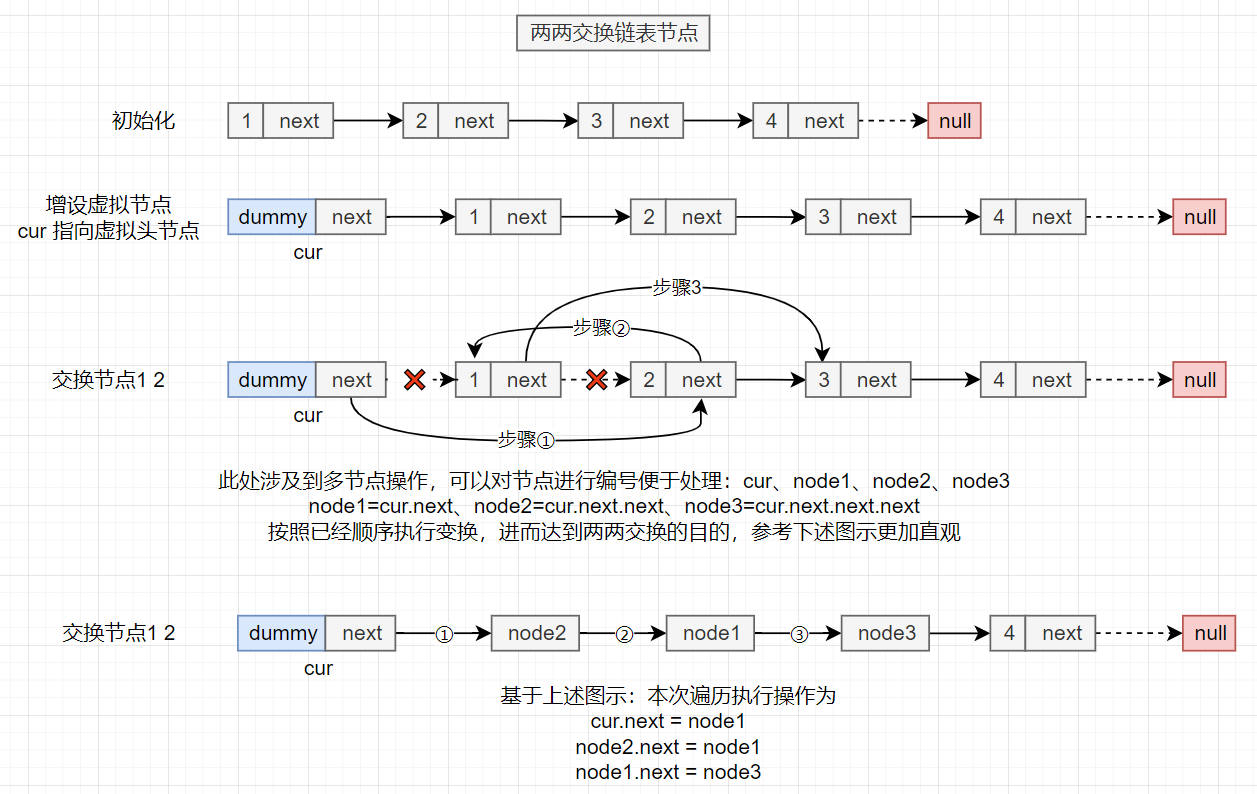
​ 参考上述分析图示，基于此进行逻辑设计即可，此处需注意步骤执行的先后顺序，以及指针移动（指针移动不是cur=cur.next 因为在这个交换过程中cur.next已经变了，所以指针遍历的下一个元素应该是一开始记录的node1）

public ListNode swapPairs(ListNode head) {
    // 增设虚拟头节点
    ListNode dummy = new ListNode(0, head);
    // 设置节点指针
    ListNode cur = dummy;

    // 遍历链表，进行元素交换(结合图示分析，链表节点交换操作需要两个元素)
    while (cur.next != null && cur.next.next != null) {
        // 记录节点信息
        ListNode node3 = cur.next.next.next;
        ListNode node1 = cur.next;
        ListNode node2 = cur.next.next;
        // 执行节点交换
        cur.next = node2;   // 步骤1
        node2.next = node1; // 步骤2 
        node1.next = node3; // 步骤3
        // 指针后移，准备下一轮交换(需注意此处cur指向的要遍历的下一个节点应为node1,而非cur.next)
        cur = node1;
    }
    // 返回链表
    return dummy.next;
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

👻方法2：递归法

​ 递归思路：先翻转前面的节点，再将翻转后的节点next指针指向节点后续链表。

​ 需要注意的是，本题的递归终点是遇到链表尾或者剩余链表中只有一个节点，这时候无法进行翻转，需要返回null或者单个节点。

class Solution {
    public ListNode swapPairs(ListNode head) {
        // 边界条件
        if(head == null || head.next == null){
            return head;
        }
        // 记录下个节点
        ListNode newNode = head.next;
        // 翻转节点
        head.next = swapPairs(newNode.next);
        newNode.next = head;
        return newNode;
    }
}

// 参考
class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head==null||head.next==null) return head;
        ListNode two = head.next;
        head.next = two.next;
        two.next = head;
        head.next = swapPairs(head.next);
        return two;
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡10-随机链表的复制（138）

1.题目内容

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝open in new window。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

2.题解思路

参考题解open in new window

​ 思路分析：这道题的含义指的是有这么一个链表节点，它包含两个指针，一个指针指向next（下一个节点），另一个指针则是指向random（指向链表中的任意节点或空节点）。如果只是普通链表的复制，那么只需要循环遍历链表直接创建新的节点（其后一个节点可以通过next进行定位）

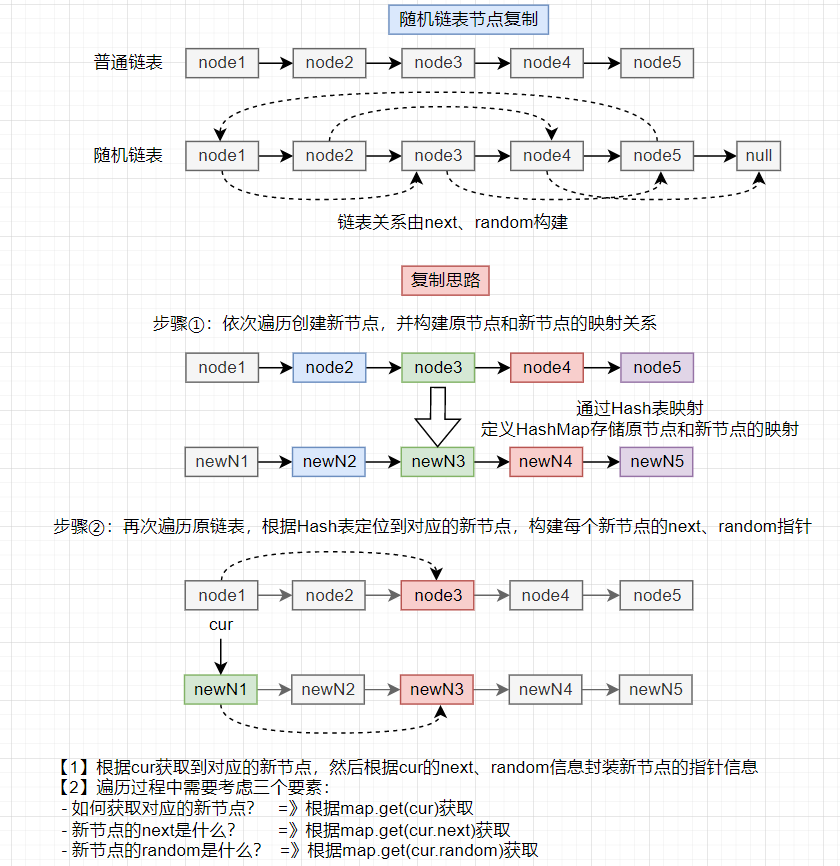
​ 但是题目中节点的设定还有一个random指针，由于random的特殊性（可以指向链表中任意节点或空节点），因此无法在一次遍历过程中就确定下来（因为如果是指向后面的节点，可能节点还没有创建出来，进而无法确定）。因此此处的题目思路可以拆分为两个步骤：步骤①先创建链表中的所有节点、步骤②根据指针关系构建节点连接

  • 步骤①：创建链表节点（暂未设定next、random指针）
    • 此处有一个设计巧思，通过定义一个HashMap将旧节点和新节点进行映射，通过这个集合就可以根据某个旧节点信息快速定位到对应的新节点
  • 步骤②：构建节点关系（依次遍历原链表，根据原指针信息确定新链表的指针关系），此处需要关注三个要素
    • 如何拿到cur对应的新节点？ =》通过map.get(cur)获取
    • newNode的next是什么？ =》通过map.get(cur.next)获取（理论上分析新节点的下一个节点应该对应为原节点的下一个节点在map的映射）
    • newNode的random是什么？ =》通过map.get(cur.random)获取（理论上分析新节点的random节点应该对应为原节点的random节点在map的映射）

image-20240927133143873

👻方法1：哈希表

​ 基于上述题解，按照步骤进行设计

public Node copyRandomList(Node head) {

    // 构建新链表
    Node res = new Node(0);

    // 定义链表指针
    Node cur = head;

    // 构建一个哈希表结构存储当前节点和对应Random节点的对应关系
    Map<Node, Node> map = new HashMap<Node, Node>();

    // 步骤①：遍历链表，用于对应创建节点（无next、random）
    // 定义哈希表
    while (cur != null) {
        Node newNode = new Node(cur.val); // 创建新节点
        map.put(cur, newNode); // 构建当前节点和新节点的映射（用于后续构建节点关系）
        cur = cur.next; // 指针后移
    }

    // 步骤②：构建链表节点之间的联系（设置next、random）
    cur = head; // 重新初始化链表指针
    while (cur != null) {
        // 根据key获取到对应的新链表节点
        Node newNode = map.get(cur);

        // 寻找这个新链表节点的next和random值

        // 设置next指针（新节点对应的next指针即为cur.next在map中的映射值）
        newNode.next = map.get(cur.next);
        // 设置random指针（新节点对应的random指针即为cur.random在map中的映射值）
        newNode.random = map.get(cur.random);

        // 指针后移
        cur = cur.next;
    }

    // 返回结果
    return map.get(head);
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡11-排序链表（148）

参考题解：可结合其他排序算法思路进行理解：常见排序算法open in new window、链表排序参考open in new window

1.题目内容

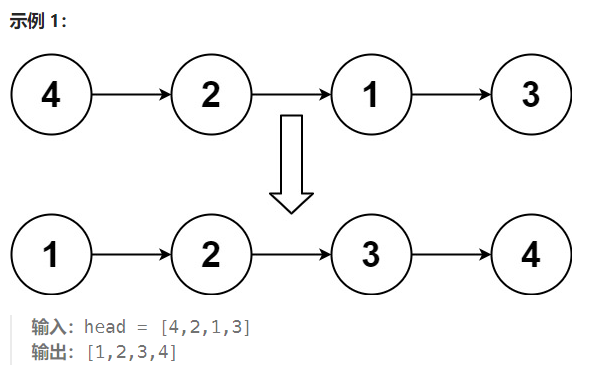
​ 给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表

image-20240927133948842

2.题解思路

👻方法1：暴力法

​ 最硬核的方式就是先遍历一遍节点，然后存入集合中，通过工具类进行排序，然后根据排序结果构建新链表

/**
 * 148-单链表排序
 * 思路1：暴力法（遍历链表节点、排序、根据排序结果回写）
 */
public class Solution1 {

    public ListNode sortList(ListNode head) {
        // 定义结果
        ListNode res = new ListNode(0);

        // 定义指针
        ListNode cur = head;

        // 定义集合存储
        ArrayList<Integer> list = new ArrayList<Integer>();

        // 步骤①：遍历链表
        while (cur != null) {
            list.add(cur.val);
            cur = cur.next; // 指针后移
        }

        // 排序
        Collections.sort(list); // 借助工具类进行排序

        // 初始化新链表指针
        cur = res;
        // 步骤②：回写链表
        for (int i : list) {
            cur.next = new ListNode(i);
            cur = cur.next;// 指针后移
        }
        // 返回结果
        return res.next;
    }

}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

🟡12-LRU缓存（146）

1.题目内容

请你设计并实现一个满足 LRU (最近最少使用) 缓存open in new window 约束的数据结构。

实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

2.题解思路

参考题解：LRU缓存算法思路open in new window

思路分析

​ 首先理解什么是LRU：Least Recently Used 最近最少使用，即当缓存域满了之后会通过这种算法优先淘汰最近最少使用的元素。

image-20240927142117278

思路1：通过访问频次大小进行淘汰

可能一般构建的思路就是类似数组存储，然后记录每个元素的访问频次：

  • 数据插入：判断是否超出阈值，如果超出阈值则淘汰访问频次最低的元素（进行替换），如果没有超出阈值则正常追加数据
  • 数据访问：更新记录访问频次

​

思路2：不设定访问频次，而是类似排队的概念，让活跃的数据排在淘汰后排

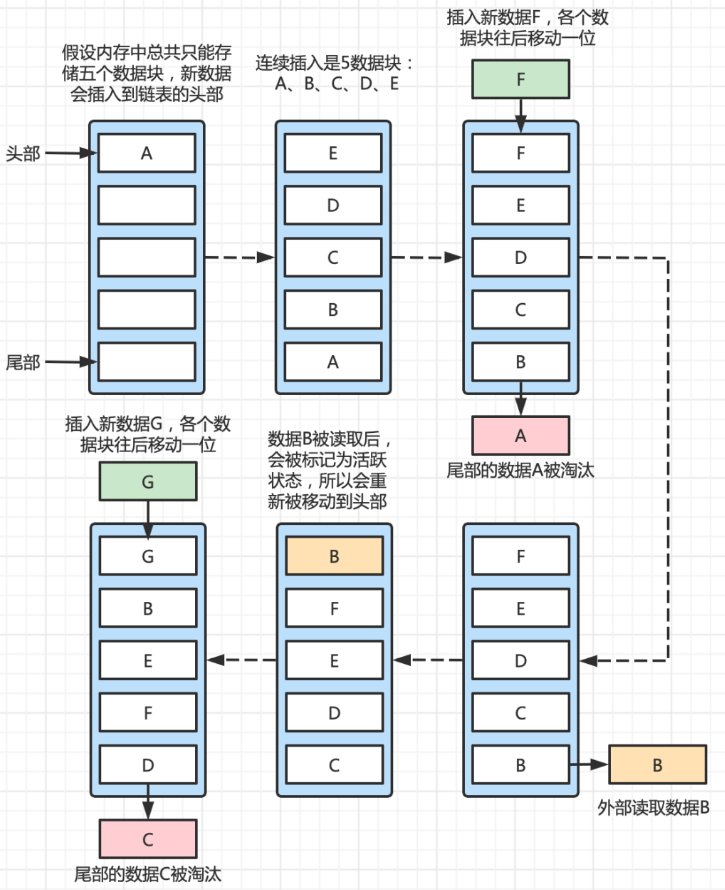
​ 基于上述流程分析，优化LRU的设计思路，如何通过不记录访问频次的方式实现LRU？即类似排队的概念，选定一个方向进行淘汰，当数据被访问时就将其重新排到后面去，以此达到不记录访问频次就能实现LRU淘汰的效果 =》淘汰尾部的数据（尾部存储的是最久远访问的数据）、让活跃的节点移动到队列另一段

  • 淘汰谁？：采用头插法，确保最新插入的数据在头部，依次类推，当依次插入数据超出缓存阈值的时候，此时尾部的数据会被淘汰（就是最先插入的数据会被淘汰）
  • 如何更新访问频次？：此处没有访问频次的概念，而是将活跃的数据移动到另一端

​ 继续剖析题目，如果get、put的时间复杂度需为O(1)，不免联想到哈希表。其次要支持在任意位置灵活地快速插入和删除元素，可借助链表。因此会联想到可以通过哈希表+链表的结构实现LRU缓存，因此初步设计数据结构为：

image-20240927145106958

​ 此处基于上述设计可以思考几个问题：

  • 为什么要使用双向链表而不是单向链表？
    • 链表的删除操作需要涉及到prev节点的next指针修改，而单向链表并没有存储前驱节点的指针，因此引入双向链表进行优化
  • 哈希表中已经存储了key，为什么链表还要存储key和value？
    • 动态删除链表节点的时候需要相应删除对应哈希表的值，因此在删除链表节点的时候可以根据存储的key到哈希表中删除节点（即根据key定位链表节点进行删除）
  • 虚拟头节点和虚拟尾节点有什么用？
    • 在链表场景中虚拟节点被广泛应用，又称为哨兵节点，通常不保存任何数据（使用虚拟节点可以统一处理链表中所有节点的插入和删除操作，而不需要考虑头、尾节点的特殊情况）

​

👻方法1：基于LinkedHashMap实现

​ 基于上述分析引入数据结构：哈希表+双向链表（JAVA中可以采用LinkedHashMap的实现），如果是算法的考察一般是要手撕双向链表的设计，而不让直接用LinkedHashMap。此处先基于LinkedHashMap理解LRU算法的实现思路

/**
 * 146-LRU缓存
 * 基于LinkedHashMap实现:存储key、value
 */
class LRUCache {

    // 定义缓存容量阈值
    int capacity ;

    // 定义数据结构（存储集合）
    LinkedHashMap <Integer, Integer> cache;

    // 构造函数
    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.cache = new LinkedHashMap<Integer, Integer>();
    }

    // 访问元素（判断元素是否存在，更新访问节点位置（重新插入：即先删后插））
    public int get(int key) {
        // 如果指定值存在
        if(cache.containsKey(key)) {
            // 记录当前值
            int value = cache.get(key);
            // 移除节点
            cache.remove(key);
            // 重新插入节点到链表尾部
            cache.put(key, value);
            return value;
        }else{
            return -1;
        }
    }

    // 插入元素（判断插入数据是否存在，存储则直接覆盖，如果不存在则继续判断是否超出阈值，超出阈值则需要触发LRU淘汰机制）
    public void put(int key, int value) {
        if(cache.containsKey(key)) {
            // key已存在则覆盖（先删后加）
            cache.remove(key);
            cache.put(key, value);
        }else{
            // 校验阈值
            if(cache.size()>=capacity){
                // 超出阈值触发清理(因为LinkedHashMap是有序的，所以此处通过迭代器获取到第一个元素，然后直接移除)
                Iterator<Integer> iterator = cache.keySet().iterator();
                cache.remove(iterator.next());
            }
            // 最终将新的数据节点插入
            cache.put(key, value);
        }
    }
}

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

3.复盘

0  字
评论
  • 按正序
  • 按倒序
  • 按热度
Powered by Waline v3.1.3
一人の境 Copyright © 2019-未知 holic-x
Copyright © 2024 holic-x