【luckydraw-ddd】领域开发03-抽奖策略领域模块开发

​ 架构分层、逻辑设计、代码流程

学习目的

【1】掌握抽奖策略领域模块开发基本流程、概念梳理（对比MVC、DDD模块开发的设计理念）

【2】掌握抽奖算法场景应用和两种不同策略算法的实现思路

【3】结合单体概率算法思路自定义实现算法逻辑基本框架

【4】学习过程问题反思、扩展、总结

1.需求分析

​ 需求：在一场营销抽奖活动玩法中，运营人员通常会配置以转盘、盲盒等展现形式的抽奖玩法。例如在转盘中配置12个奖品，每个奖品配置不同的中奖概率，当1个奖品被抽空了以后，那么再抽奖时，是剩余的奖品总概率均匀分配在11个奖品上，还是保持剩余11个奖品的中奖概率，如果抽到为空的奖品则表示未中奖。其实这两种方式在实际的运营过程中都会有所选取，主要是为了配合不同的玩法。

​ 设计：在做这样的抽奖领域模块设计时，就要考虑到库表中要有对应的字段来区分当前运营选择的是什么样的抽奖策略。那么在开发实现上也会用到对应的策略模式的使用，两种抽奖算法可以算是不同的抽奖策略，最终提供统一的接口包装满足不同的抽奖功能调用

​ 实现：在实现上让抽奖策略成为独立配置使用的领域模块，从而避免被业务逻辑污染，满足不同业务场景的灵活调用。例如：有些业务场景是需要你直接来进行抽奖反馈中奖信息发送给用户，但还有一些因为用户下单支付才满足抽奖条件的场景对应的奖品是需要延时到账的，避免用户在下单后又进行退单，这样造成了刷单的风险。

2.项目结构设计

​ 抽奖系统工程采用DDD架构 + Module模块方式搭建，lottery-domain 是专门用于开发领域服务的模块，不限于目前的抽奖策略在此模块下实现还有以后需要实现的活动领域、规则引擎、用户服务等都需要在这个模块实现对应的领域功能。

架构分层

概念梳理

​ 结合传统MVC架构、模块化开发、DDD领域概念理解“领域服务”概念，结合下图所示进行分析

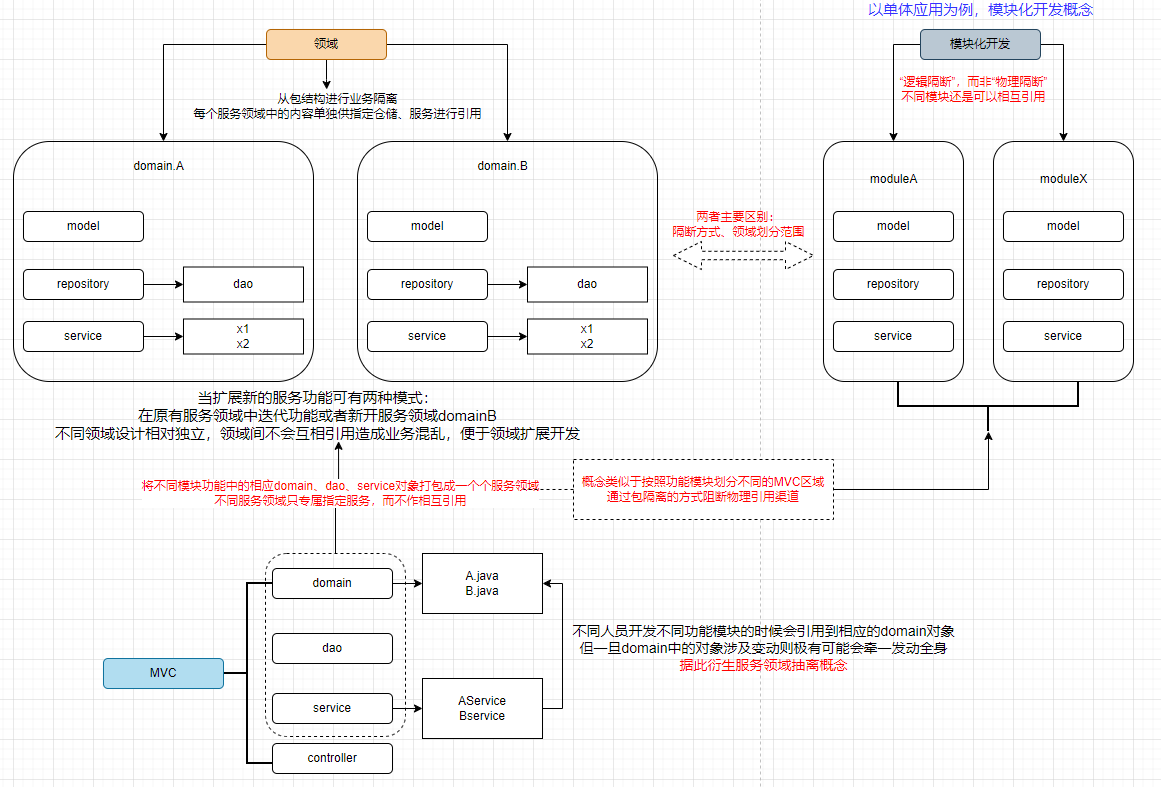
​ 【1】传统MVC结构对代码进行分层（model、dao、service），不同人员开发不同功能模块的时候会引用到相应的domain对象 但一旦domain中的对象（此处的domain概念可以泛化理解为model、dao、dto、vo等对象定义）涉及变动则极有可能会牵一发动全身，不同模块之间相互引用并不利于业务解耦和扩展，据此衍生服务领域抽离概念

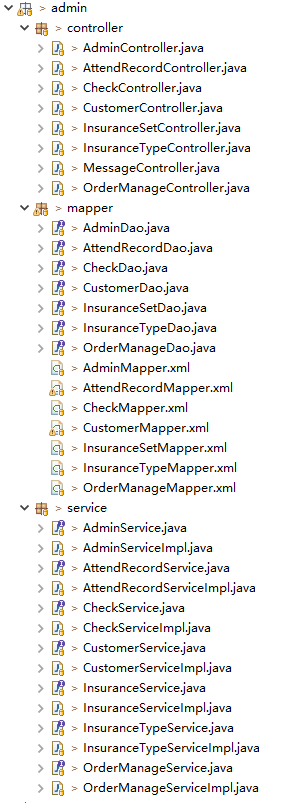
​ 参考下述工程项目，将后台管理功能中所有模块糅杂在一起，不同模块间存在相互引用的情况，并不利于业务解耦和迭代扩展

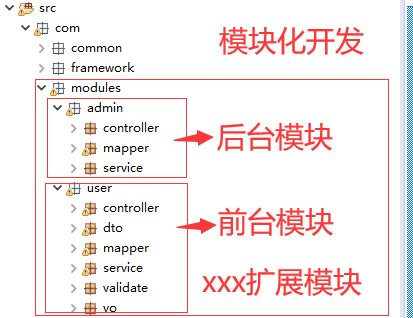
​ 【2】以单体应用开发为例，为了进一步划分功能模块开发的职责，通常会以“模块化开发”概念为基础，按照业务功能或者其他分类标准划分不同的包结构从而区分开发领域（以项目示例：按照不同功能模块划分包区域、在此基础上还可细化模块功能开发），但还是不可避免模块间的相互引用，以及后续业务迭代升级的联动变更

​ 【3】“领域服务”的构建则是基于上述场景衍生的产物，按照一定的规则划分服务领域概念，将相应的domain、dao、service对象打包成一个领域服务概念，不同领域服务只专属于某个服务而不相互引用，可从两个角度进一步理解概念：

​ 物理隔断概念，不同领域服务之间不相互引用，相互之间迭代升级不存在联动变更的情况

​ 领域划分更为精细，结合相应的业务场景细化领域服务概念（可细化到某个功能概念），其主要目的在于业务解耦、迭代升级

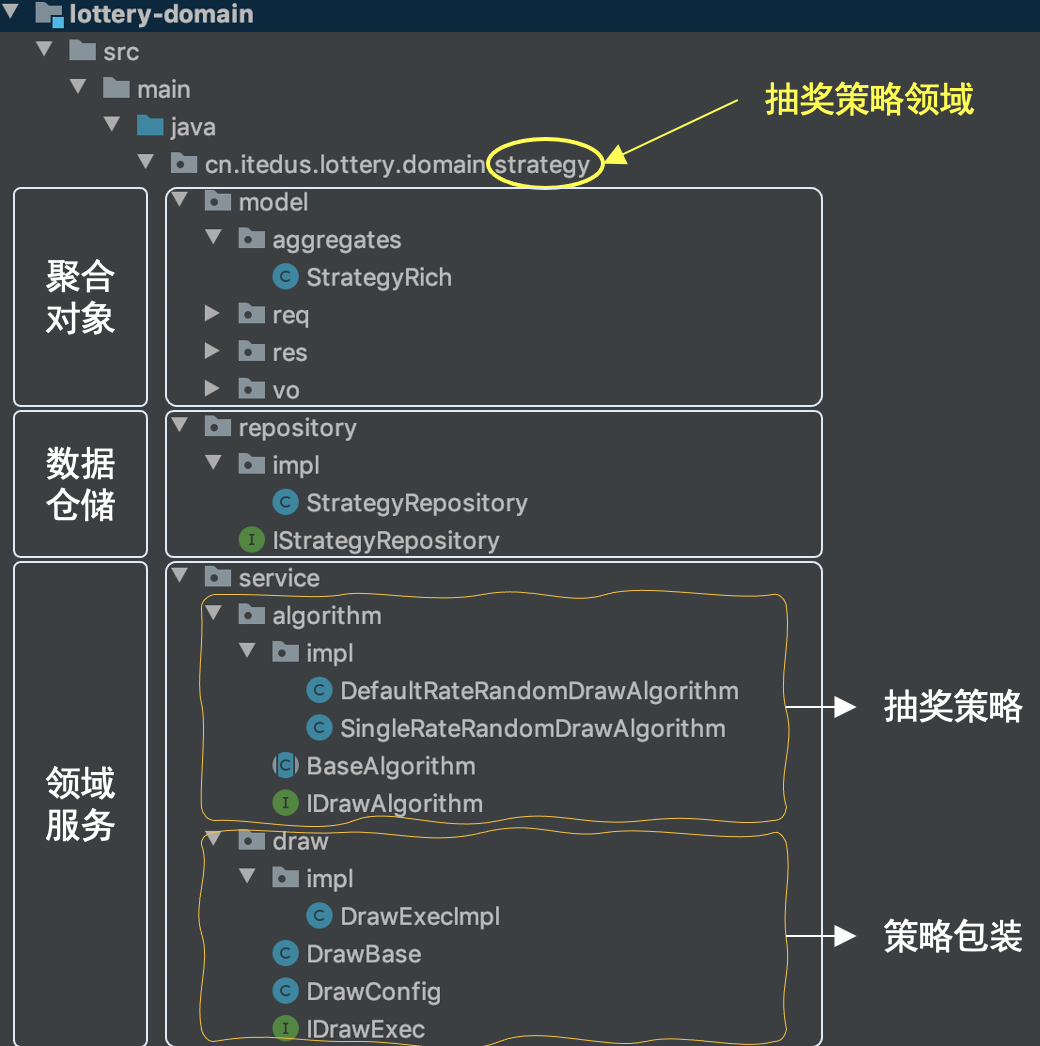
​ strategy 是在 domain 下实现的抽奖策略领域，在领域功能开发的服务下主要含有model、repository、service三块区域：

• model，用于提供vo、req、res 和 aggregates 聚合对象
• repository，提供仓储服务（对Mysql、Redis等数据的统一包装）
• service，具体的业务领域逻辑实现层（定义了algorithm抽奖算法实现和具体的抽奖策略包装 draw 层，对外提供抽奖接口 IDrawExec#doDrawExec）

---

TO DO：

​ 公共模块概念抽离的标准有哪些？

​ 虽然实现业务解耦，便于迭代升级，但基于这种方式会不会显得体系过于臃肿、维护成本等问题？这种实际业务中领域服务划分的参考标准有哪些？进一步了解DDD在业务快速迭代开发场景中的应用

---

逻辑设计

​ 抽奖策略相关的算法：斐波那契抽奖算法

抽奖策略实现方式1

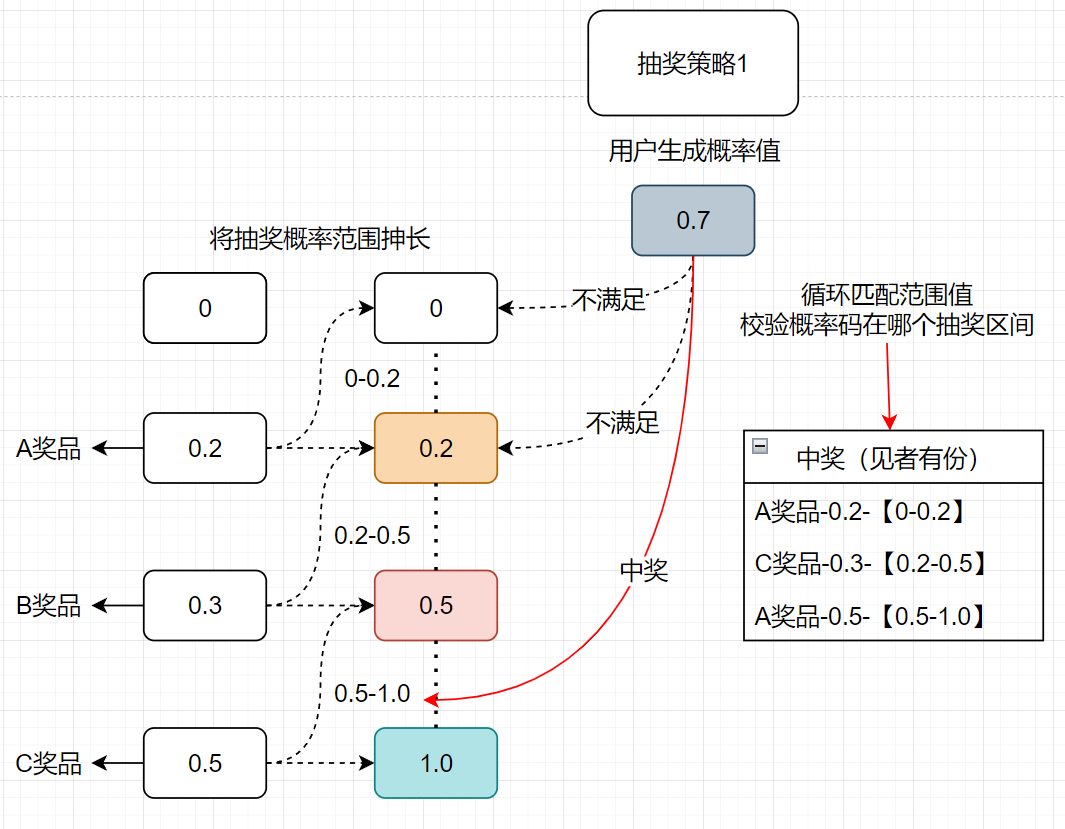
​ 给各个奖品设定相应的中奖概率，将根据概率划分相应的中奖区域（将抽奖概率范围抻长），用户生成概率码，随后算法校验概率码所在的抽奖区间从而匹配相应的奖品，算法时间复杂度O（n）

抽奖策略实现方式2

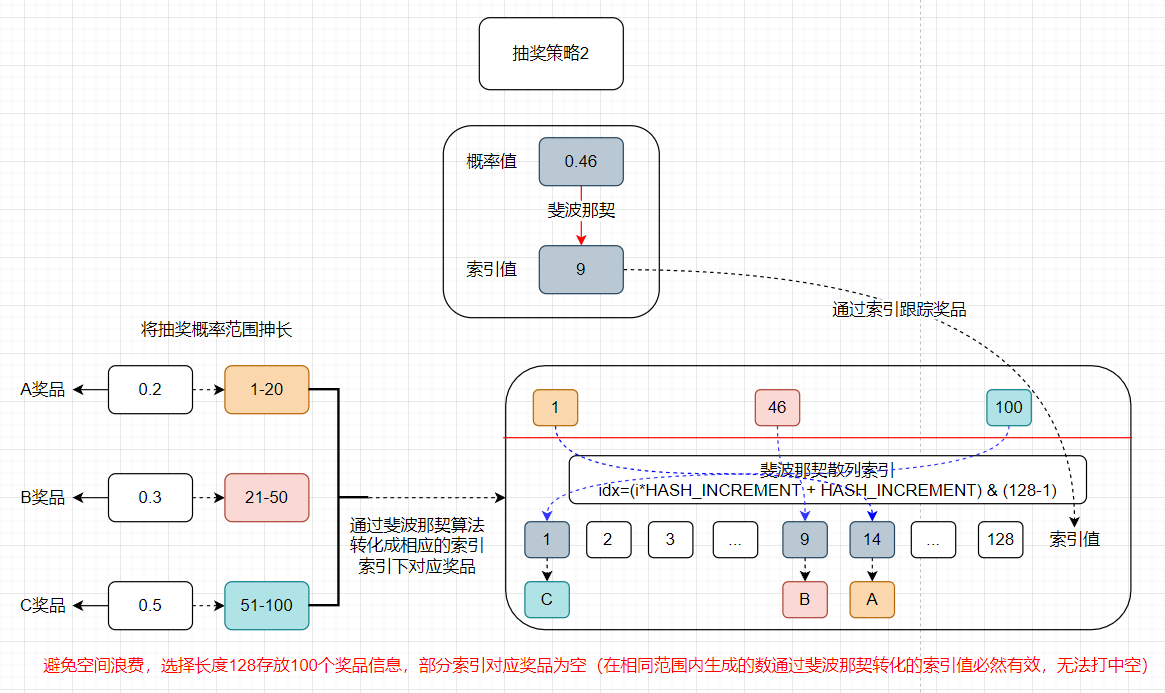
​ 给各个奖品设定相应的中奖概率，还是相应抻长中奖概率范围，针对每个数字通过斐波那契算法转化成相应的索引值，对应索引值指向相应的奖品信息。用户进行抽奖是生成相应的概率值，随后通过斐波那契算法转化获取相应的索引，再根据索引找到该索引指向的奖品信息。算法时间复杂度O(1)

---

TODO：

​ 斐波那契为什么能散列数据而不发生碰撞，HashMap计算可能产生哈希碰撞（碰撞后通过拉链寻址、红黑树概念）

​ 为什么用“斐波那契”：斐波那契实现利用最小空间、黄金分割点增量计算、均匀散列数据而不碰撞

​ HashMap负载因子决定hash桶的高矮胖瘦，在尽量避免碰撞的前提下可能需要更大的空间

---

代码实现

构建过程

工程	说明
lottery	pom.xml引入dependencyManagement标签，对依赖版本进行统一管理
lottery-infrastructure	引入抽奖策略相关dao、po定义
lottery-domain	pom.xml引入相关依赖 抽奖策略领域模块开发（model、repository、service）
数据库	数据初始化（策略、奖品信息等）

【1】重温策略模式

代码设计思路

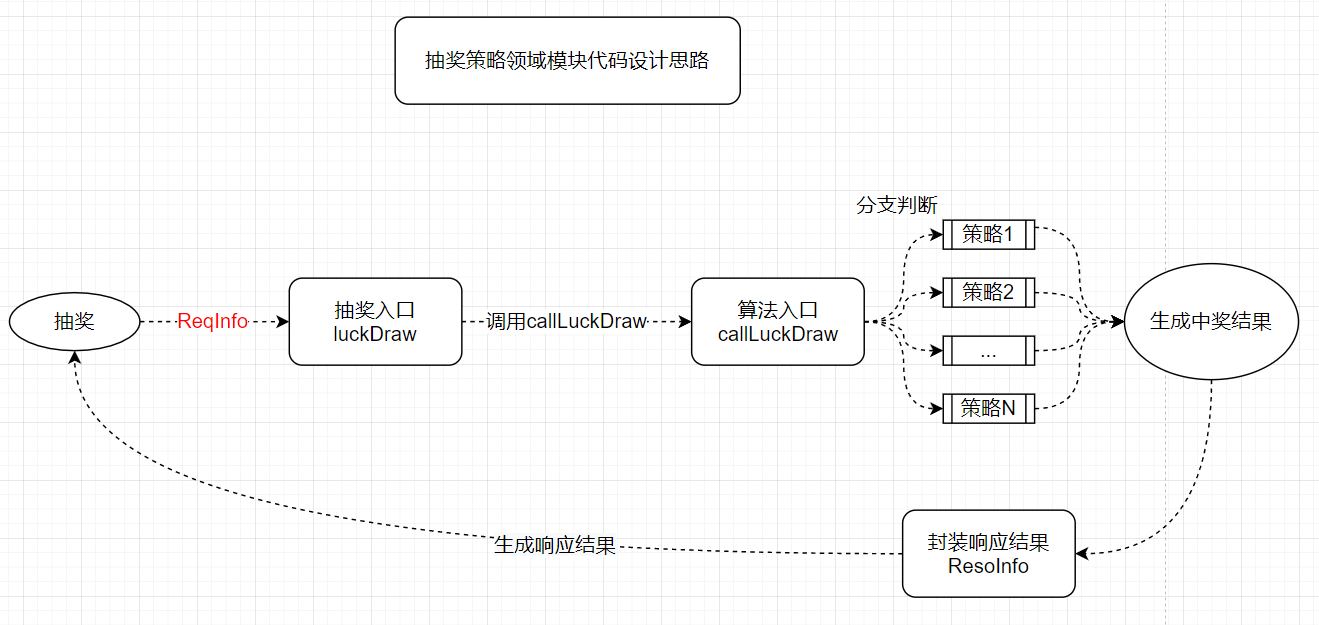
​ 结合上述算法设计分析，梳理基本代码框架有如下代码设计思路：

1.构建抽奖入口（接收用户请求参数：用户id-uId、策略id-strategyId:将请求参数封装为一个ReqInfo实体便于扩展）
	用户通过指定策略生成概率码，调用相应的算法进行抽奖
2.构建算法入口（接收策略id，调用相应的算法实现）
	方式1：通过if-else对策略id进行判断，随后调用相应的算法实现
	方式2：通过策略模式抽离
3.获取到抽奖结果，封装中奖信息并返回结果

// --------------- 伪代码说明 ------------------------
// 1.抽奖入口
public RespInfo luckDraw(ReqInfo reqInfo){
	// <1>接收用户请求
	
	// <2>调用算法获取中奖结果
	String res = callLuckDraw(strategyId);

	// <3>封装响应结果
	RespInfo respInfo = new RespInfo();
	respInfo.setXXX(xxx);
} 

// 算法入口
public String callLuckDraw(String strategyId){
	// 根据strategyMode判断调用的算法策略
	if("1".equals(strategyId)){
		// 算法1......	
		return algorithm1();
	}else if("2".equals(strategyId)){
		// 算法2
		return algorithm2();
	}else{
		// 其余情况判断
	}
}

策略模式重构代码设计

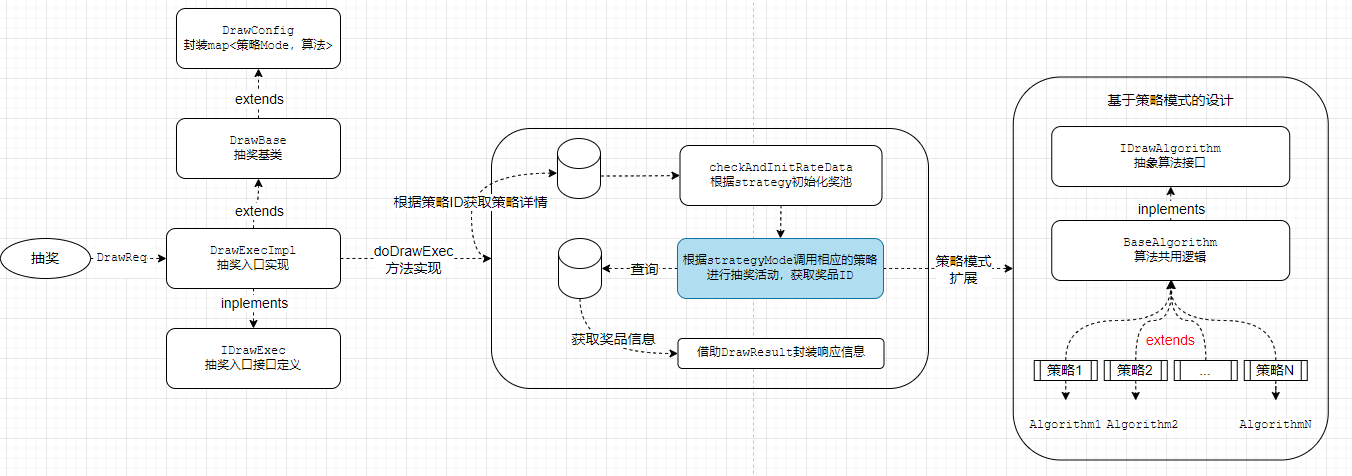
# 基于上述设计思路，在扩展新的算法代码时，则可依据下述步骤进行扩展
<1> 自定义抽奖算法CustomRandomDrawAlgorithm继承BaseAlgorithm并重载randomDraw方法（根据自己的算法逻辑实现抽奖）
<2> DrawConfig中装载自定义算法，将其载入map集合中 
<3> 业务调用说明:DrawExecImpl中会根据strategyMode调用相应的算法获取抽奖结果（奖品ID）（此处不需要做变更）

// 代码实现说明
<1> 自定义抽奖算法CustomRandomDrawAlgorithm继承BaseAlgorithm并重载randomDraw方法（根据自己的算法逻辑实现抽奖）
public class CustomRandomDrawAlgorithm extends BaseAlgorithm {
    @Override
    public String randomDraw(Long strategyId, List<String> excludeAwardIds) {
        // ------ 自定义抽奖算法实现抽奖，返回awardId ------
        return null;
    }
}
  
<2> DrawConfig中装载自定义算法，将其载入map集合中 
public class DrawConfig {

    @Resource
    private IDrawAlgorithm defaultRateRandomDrawAlgorithm;

    @Resource
    private IDrawAlgorithm singleRateRandomDrawAlgorithm;

    // 自定义算法引入
    @Resource
    private CustomRandomDrawAlgorithm customRandomDrawAlgorithm;

    protected static Map<Integer, IDrawAlgorithm> drawAlgorithmMap = new ConcurrentHashMap<>();

    @PostConstruct
    public void init() {
        drawAlgorithmMap.put(1, defaultRateRandomDrawAlgorithm);
        drawAlgorithmMap.put(2, singleRateRandomDrawAlgorithm);
      	// 将自定义算法载入map<策略Mode,自定义算法>
        drawAlgorithmMap.put(3, customRandomDrawAlgorithm);
    }

}

// PS:此处strategyMode可通过自定义枚举类进行数据封装便于统一管理

【2】抽奖策略动态引入改造

​ 上述方式在扩展策略的时候需要通过手动注册的方式实现，参考issue中大佬们提出的方案采用自定义注解+枚举+扫描配置的方式改造抽奖策略的扩展

改造说明

【1】创建StrategyModeEnum统一策略模式管理

【2】创建自定义注解StrategyMode

【3】在自定义抽奖策略实现类中引入自定义注解@StrategyModeEnum

【4】修改抽奖策略注册的方法，动态注入自定义策略实现

【1】创建StrategyModeEnum统一策略模式管理

// package cn.itedus.lottery.common; 在lottery-common中实现

/**
 * 抽奖策略枚举
 * 策略id、策略描述（可扩展策略其他属性）
 */
public enum StrategyModeEnum {

    DEFAULT_RATE_RANDOM_DRAW_ALGORITHM(1,"必中奖策略抽奖，排掉已经中奖的概率，重新计算中奖范围"),
    SINGLE_RATE_RANDOM_DRAW_ALGORITHM(2,"单项随机概率抽奖，抽到一个已经排掉的奖品则未中奖"),
		// 自定义扩展引入新的抽奖策略
  	CUSTOM_RATE_RANDOM_DRAW_ALGORITHM(3,"自定义扩展引入新的抽奖策略");
  
    ;
    private StrategyModeEnum(Integer id,String description){

    }

    /**
     * 策略id
     */
    private Integer id;

    /**
     * 策略描述
     */
    private String description;

    public Integer getId() {
        return id;
    }

    public String getDescription() {
        return description;
    }
}

【2】创建自定义注解StrategyMode

// package cn.itedus.lottery.domain.strategy.annotation; 在lottery-domain对应领域中实现
/**
 * 自定义抽奖策略模型注解
 */
@Target({ElementType.TYPE})
@Retention(RetentionPolicy.RUNTIME)
public @interface StrategyMode {

    /**
     * 抽奖策略模型枚举
     */
    StrategyModeEnum strategyMode();
}

【3】在自定义抽奖策略实现类中引入自定义注解@StrategyModeEnum

/**
 * 自定义算法实现抽奖（引入注解）
 */
@Component("CustomRandomDrawAlgorithm")
@StrategyMode（strategyMode=StrategyModeEnum.CUSTOM_RATE_RANDOM_DRAW_ALGORITHM）
public class CustomRandomDrawAlgorithm extends BaseAlgorithm {
    @Override
    public String randomDraw(Long strategyId, List<String> excludeAwardIds) {
        // 自定义抽奖算法实现抽奖，返回awardId
        return null;
    }
}

【4】修改抽奖策略注册的方法，动态注入自定义策略实现

//package cn.itedus.lottery.domain.strategy.service.draw; lottery-domain中strategy领域实现
public class DrawConfig implements ApplicationContextAware {
    private ApplicationContext applicationContext;
    protected static Map<Integer, IDrawAlgorithm> drawAlgorithmMap = new ConcurrentHashMap<>();

    @PostConstruct
    public void init() {
      	// 扫描包含指定注解的组件，动态注入 
        Map<String, Object> strategyModeMap = applicationContext.getBeansWithAnnotation(
            StrategyMode.class);
        strategyModeMap.entrySet().forEach(r->{
            StrategyMode strategyMode = AnnotationUtils.findAnnotation(r.getValue().getClass(),StrategyMode.class);
            if(r.getValue() instanceof IDrawAlgorithm){
                drawAlgorithmMap.put(strategyMode.strategyMode().getId(), (IDrawAlgorithm)r.getValue());
            }
        });
    }
    /**
     * 注入 ApplicationContext
     */
    @Override public void setApplicationContext(ApplicationContext applicationContext) throws BeansException 
    {
        this.applicationContext = applicationContext;
    }
}

新的抽奖策略添加

（1）在StrategyModeEnum引入新的策略模式

（2）在自定义抽奖策略实现类中引入自定义注解@StrategyModeEnum

算法设计思路学习

两种抽奖算法描述，场景A20%、B30%、C50%

• 总体概率：如果A奖品抽空后，B和C奖品的概率按照 3:5 均分，相当于B奖品中奖概率由 0.3 升为 0.375
• 单项概率：如果A奖品抽空后，B和C保持目前中奖概率，用户抽奖扔有20%中为A，因A库存抽空则结果展示为未中奖。（为了节省运营成本，通常这种情况的使用的比较多）

【1】总体概率（算法）

​ 算法描述：分别把A、B、C对应的概率值转换成阶梯范围值，A=(0~0.2」、B=(0.2-0.5」、C=(0.5-1.0」，当使用随机数方法生成一个随机数后，与阶梯范围值进行循环比对找到对应的区域，匹配到中奖结果。

【2】单体概率（算法）

​ 算法描述：单项概率算法不涉及奖品概率重新计算的问题，即分配好的概率结果是可以固定下来的。尝试实现一个可以优化的算法，不需要在轮训匹配O(n)时间复杂度来处理中奖信息，而是可以根据概率值存放到HashMap或者自定义散列数组进行存放结果，这样就可以根据概率值直接定义中奖结果，时间复杂度由O(n)降低到O(1)。这样的设计在一般电商大促并发较高的情况下，达到优化接口响应时间的目的。

# 算法构建思路
<1> 定义一个HashMap<String,String>初始化存储<索引值,奖品ID>-awardMap（或者用数组实现存储,下标即索引）
<2> 实现randomDraw方法:
	a.随机生成一个概率码，通过斐波那契散列法获取相应的索引
	b.从awardMap中获取指定的索引对应的value(奖品类型)
	c.根据奖品类型判断当前奖池中是否存在奖品剩余，如果有则表示中奖（随机取对应类型的奖品ID并发放，调整奖品发放状态），如果没有则表示未中奖
<3>返回奖品ID（中奖则返回奖品ID，未中奖则返回null）

/**
 * 自定义单体概率算法（此处针对场景描述算法设计实现思路，暂不嵌入策略模式）
 * 因为仅从基础框架中大概了解抽奖算法的基本设计思路，但具体的策略模板详细内容和奖品设定规则还未明确，
 * 因此此处针对场景描述单体概率算法设计的实现思路，构建大致设计轮廓，暂不嵌入策略模式，待后续进一步扩展完善
 */
public class CustomSingleRateRandomDrawAlgorithm {

    // 斐波那契散列增量，逻辑：黄金分割点：(√5 - 1) / 2 = 0.6180339887，Math.pow(2, 32) * 0.6180339887 = 0x61c88647
    private final int HASH_INCREMENT = 0x61c88647;

    // 数组初始化长度
    private final int RATE_TUPLE_LENGTH = 128;

    public HashMap<String,String> awardMap = new HashMap<>() ;

    /**
     * 根据随机数获取散列索引值
     */
    public int hashIdx(int val) {
        int hashCode = val * HASH_INCREMENT + HASH_INCREMENT;
        return hashCode & (RATE_TUPLE_LENGTH - 1);
    }

    /**
     * 初始化奖池（指定随机幸运数范围初始化集合存储索引和对应奖品ID）
     */
    public void init(){
        // 模拟100个奖品
        for(int i=1;i<=100;i++){
            // 索引、奖品
            awardMap.put(String.valueOf(hashIdx(i)),"奖品"+i);
        }
    }

    /**
     * 模拟校验奖品状态
     */
    private boolean validAwardStatus(){
        return true;
    }

    /**
     * 自定义单体概率算法模拟抽奖
     */
    public String randomDraw(){
        // 随机生成指定范围以内的数字，并获取对应数字的索引值
        int randomVal = new SecureRandom().nextInt(100) + 1;
        int idx = hashIdx(randomVal);

        // 根据生成的索引校验奖池中是否有相应的奖品信息(根据指定类型传入参数，否则校验结果存在异常)
        String award = awardMap.get(String.valueOf(idx));
        if(!StringUtils.isEmpty(award)){
            // 模拟从数据库中校验奖品状态（如果奖品已经被其他用户锁定则当前用户没有中奖）
            return validAwardStatus()?award:"很遗憾，该奖品已被锁定";
        }

        return "没有中奖哦";
    }

    /**
     * 业务调用模拟
     */
    public String luckyDraw(){
        // 初始化奖池信息
        init();
        // 调用算法模拟抽奖
        return randomDraw();
    }

    public static void main(String[] args) {

        /**
         * 一般调用步骤
         * a.根据用户ID、策略ID获取相应的策略模板详情
         * b.根据策略模板参数封装奖池信息、调用相应的算法
         * c.返回封装结果
          */

        CustomSingleRateRandomDrawAlgorithm csrd = new CustomSingleRateRandomDrawAlgorithm();
        // 测试：初始化奖池，根据策略模板参数封装奖池信息、调用相应的算法
        csrd.init();
        for(int i=0;i<1000;i++){
            System.out.println("第"+i+"次抽奖，中奖结果为："+csrd.luckyDraw());
        }

    }

}

3.问题思考

随机摇号问题

​ 从上述抽奖算法理解来看，是将一定数量的奖品通过斐波那契散列法获取相应的索引并落在对应的数组中，随后抽奖随机生成一个概率码（数字）亦通过斐波那契散列法获取相应的索引然后对照奖品；如果简化成将奖品直接按照相应比例落在数组不同位置（对应索引即为中奖号码），用户摇号直接根据范围内随机生成的数据对照数据校验结果，其时间复杂度也是O(1)，这两种方式实现上怎么考虑优缺性？

​ 分析：从上问题分析可知，可从去多个维度考虑这个问题，一是技术扩展性（从抽奖算法设计的价值点考虑，可多扩展了解一些应用和场景），二是抽奖概率分布问题（如果采用后者简化是否存在概率单一性的风险，这点得根据随机数生成的原理去分析），三是考虑是否存在一种概率相对平等的随机数生成方法（扩展了解JAVA随机数生成的不同方式以及对应的优缺点）

Java中常用的随机数生成

• 方式1：通过System.currentTimeMillis()来获取一个当前时间毫秒数的long型数字
• 方式2：通过Math.random()返回一个0到1之间的double值
• 方式3：通过Random或者SecureRandom

JDK8中源码对Random有如下解释

• Random 类使用线性同余法 linear congruential formula 来生成伪随机数

• 两个 Random 实例，如果使用相同的种子 seed，则产生的随机数序列也是一样的

// 测试案例
public class RandomTest {

    public static void main(String[] args) {
        // 不指定种子：Random默认使用系统时钟生成种子seed，所以每次获取的随机数不同
        Random random = new Random();
        System.out.println("\n default random生成结果：");
        for(int i = 0;i<10;i++){
            System.out.print(random.nextInt()+ "***");
        }
        // 指定种子：如果不同实例指定的seed相同则其生成随机数结果相同
        Random r1 = new Random(10);
        Random r2 = new Random(10);
        System.out.println("\n r1(指定seed)第一次生成结果：");
        for(int i = 0;i<10;i++){
            System.out.print(r1.nextInt() + "***");
        }
        System.out.println("\n r1(指定seed)第二次生成结果：");
        for(int i = 0;i<10;i++){
            System.out.print(r1.nextInt() + "***");
        }
        System.out.println("\n r2(指定seed)生成结果：");
        for(int i = 0;i<10;i++){
            System.out.print(r2.nextInt() + "***");
        }
    }
}

• Random 是线程安全的，程序如果对性能要求比较高的话，推荐使用 ThreadLocalRandom

• Random 不是密码学安全的，加密相关的推荐使用 SecureRandom

真随机&伪随机

​ 随机数可以用于各种目的，例如生成数据加密密钥、模拟和建模复杂现象以及从更大的数据集中选择随机样本。使用计算机生成随机数的主要方法有两种:伪随机数生成器(PRNGs)和真随机数生成器(TRNGs)

​ 大部分程序和语言中的随机数都是伪随机概念，是由可确定的函数（例如线性同余），通过一个种子（常用时钟）产生的。即如果知道了种子，或者已经产生的随机数，都可能获得接下来随机数序列的信息（具备可预测性）。

​ 与PRNGs相比，TRNGs从物理现象中提取随机性并将其引入计算机，将程序、代码等想象成一个封闭的空间，引入空间外部的变量。以Unix内核中随机数发生器(/dev/random)为例子，其Unix 维护了一个熵池，不断收集非确定性的设备事件，即机器运行环境中产生的硬件噪音，来作为种子（例如时钟、IO 请求的响应时间、特定硬件中断的时间间隔、键盘敲击速度、鼠标位置变化等周边物理环境或其他导致的不确定因素都可能被用来生成随机数）

​ 程序和算法本身不能产生真随机，但可通过迂回的方式实现统计意义上的真随机

​ 程序设计中针对实际的应用场景选择合适的随机数生成方式，例如在数据加密、抽奖、赌博、游戏、随机样本等场景中往往需要“真随机数”生成，而针对一些数据模拟、模型构建等场景则结合需求选择合适的随机数生成方式

---

​ // TODO

​ 随机数生成规则、概率问题分析

---