常用排序算法

学习核心

学习资料

• 菜鸟笔记-十大经典排序算法
• 十二种排序算法

排序算法

​ 此处排序算法的演示均按照升序进行处理

1.冒泡排序

​ 冒泡排序核心：循环遍历数组，依次比较两个相邻的元素，按照递增或者递减的规则决定元素的交换，将当前轮次的min或max交换到数组末尾

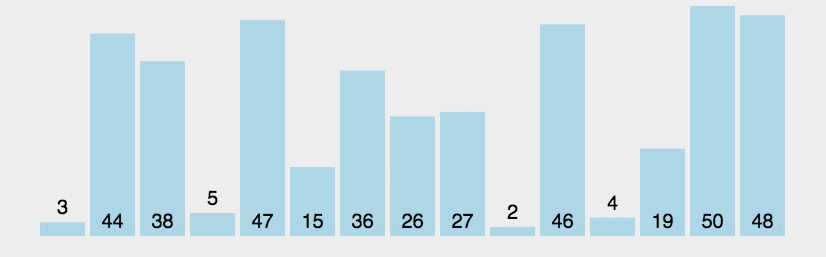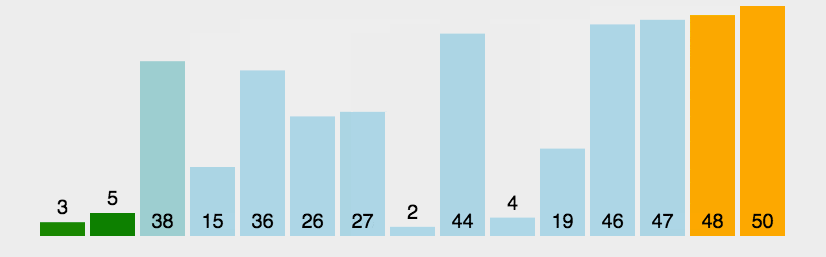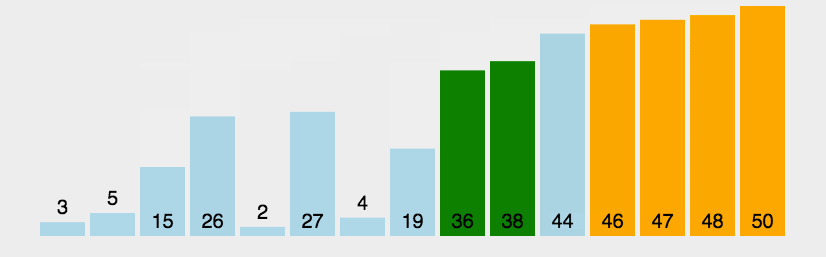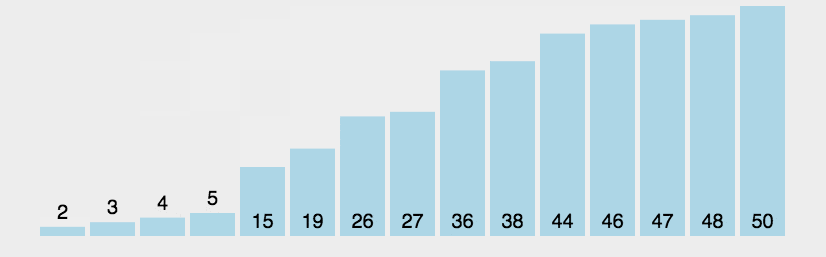
public class BubbleSort {
    /**
     * 冒泡排序算法
     */
    public int[] bubbleSort(int[] arr) {
        // 冒泡：循环遍历数组，依次比较两个相邻的元素，按照递增或者递减的规则决定元素的交换，将当前轮次的min或max交换到数组末尾
        for(int i = 0; i < arr.length - 1; i++) {
            // 依次比较相邻两个元素（此处边界设定考虑有两个因素：一是相邻两个元素比较，二是数组尾部的是前面轮次放置的最大值，因此在后面的轮次中无需重复比较）
            for(int j = 0; j < arr.length - i - 1; j++) {
                if(arr[j] > arr[j + 1]) {
                    // 将较大的元素交换到后面
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        // 返回排序后的数组
        return arr;
    }

    public static void main(String[] args) {
        int[] arr = { 3, 5, 15, 26, 27, 2, 36 };
        BubbleSort bubbleSort = new BubbleSort();
        Arrays.stream(bubbleSort.bubbleSort(arr)).forEach(System.out::println);
    }
}

2.选择排序

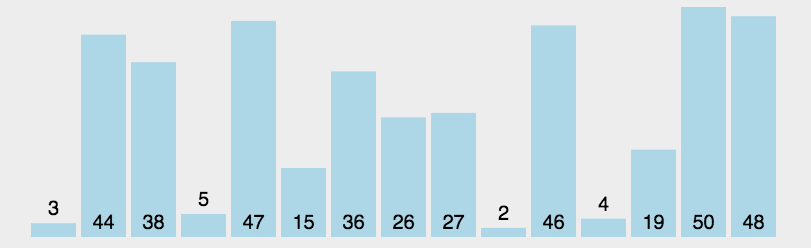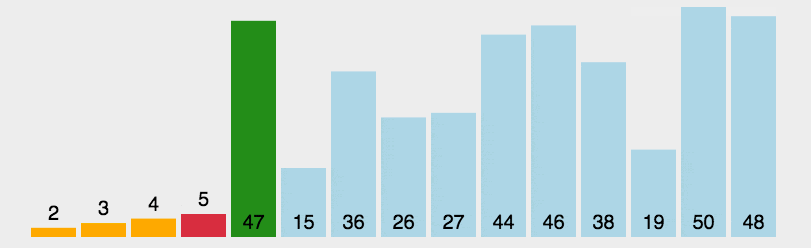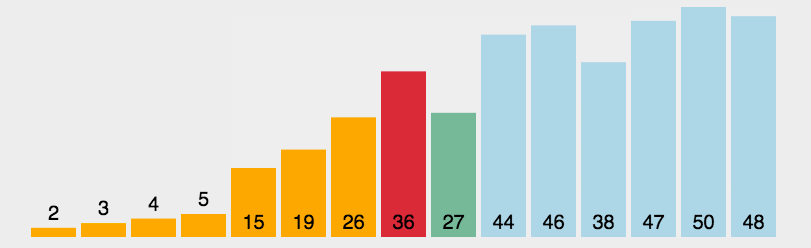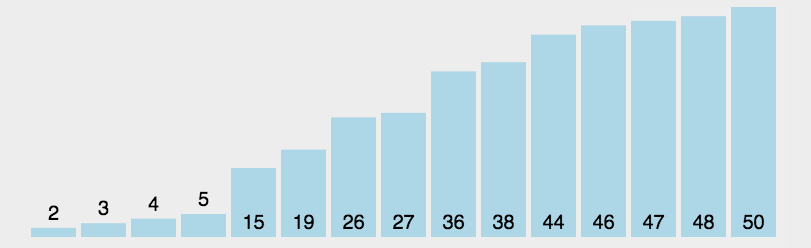
public class SelectionSort {

    /**
     * 选择排序算法(基础)
     */
    public int[] selectionSortBase(int[] arr) {
        // 选择：每一轮都将当前元素和其后面的元素进行比较，按照升序或降序的要求进行数据交换
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    // 将较大的元素交换到后面
                    int temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        // 返回排序后的数组
        return arr;
    }


    /**
     * 选择排序算法(优化)
     * 选择排序实际在每一轮比较中选择的是当前轮次（当前元素所在位置之后的元素）的min或max，最终交换也是将这个最值和当前轮次索引位置进行交换
     * 因此对于过程中的比较可以记录这个最值索引，然后在当前轮次结束后执行一次交换即可（省略过程中一些不必要的交换）
     */
    public int[] selectionSort(int[] arr) {
        // 选择：循环遍历数组，依次比较两个相邻的元素，按照递增或者递减的规则决定元素的交换，将当前轮次的min或max交换到数组末尾
        for (int i = 0; i < arr.length - 1; i++) {
            // 初始化当前轮次的最小值
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[minIndex] > arr[j]) {
                    // 更新当前轮次的最值索引
                    minIndex = j;
                }
            }
            // 一轮比较结束之后执行交换（如果minIndex!=i说明最小值索引更新了需要执行交换操作）
            if(minIndex != i) {
                int temp = arr[minIndex];
                arr[minIndex] = arr[i];
                arr[i] = temp;
            }
        }
        // 返回排序后的数组
        return arr;
    }
}

3.插入排序

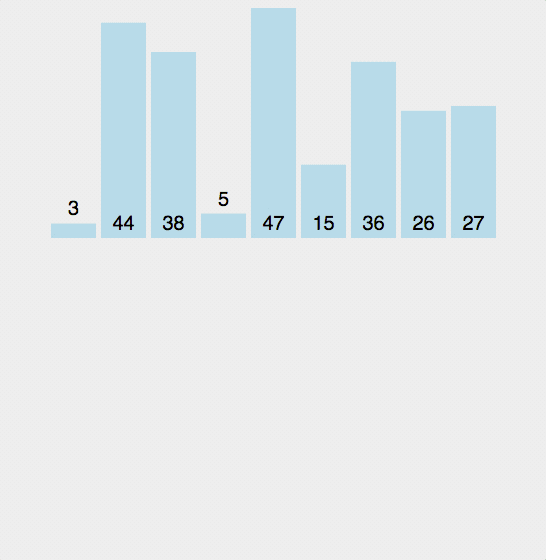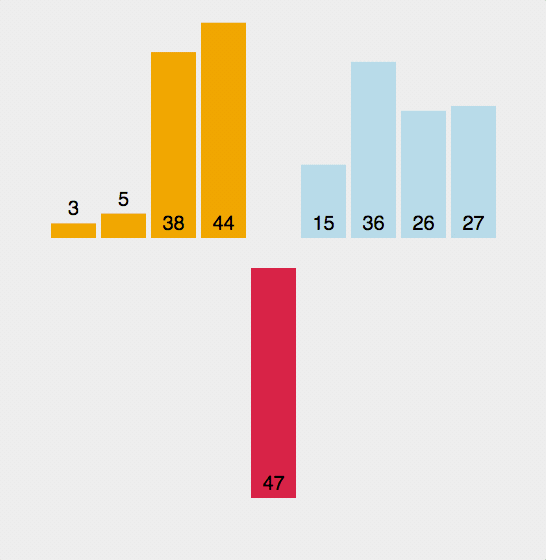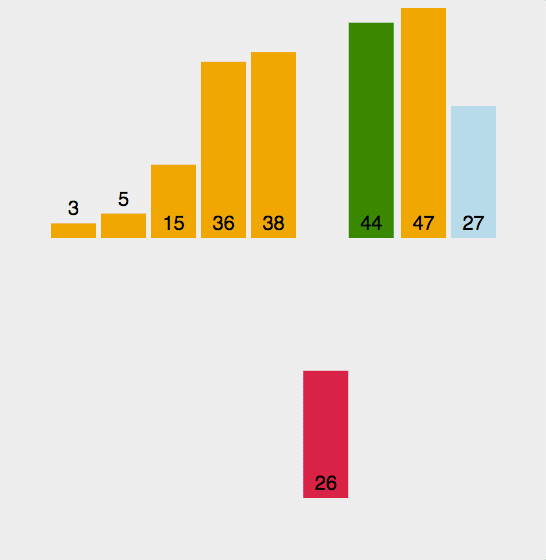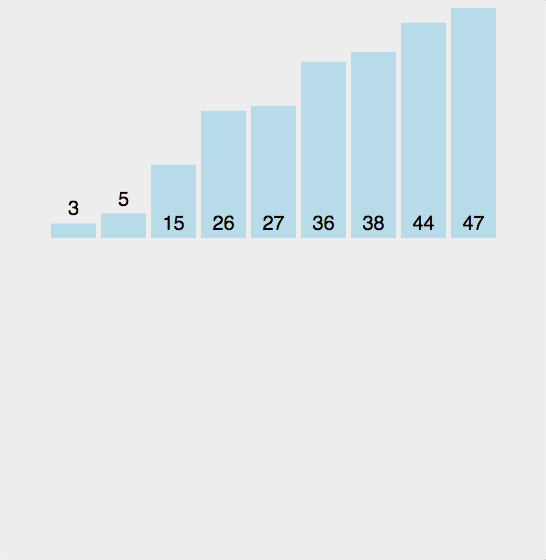
public class InsertionSort {
    /**
     * 选择排序算法(基础)
     */
    public int[] selectionSortBase(int[] arr) {
        // 插入：类似排扑克牌的思路，
        // 外循环：已排序区间为 [0, i-1]（i位置前面的元素已经完成排序）
        for (int i = 1; i < arr.length; i++) { // 从第2个元素开始执行第1轮插入
            // 待插入元素
            int curKey = arr[i];
            // 待插入位置（起始从i-1位置开始往前进行比较，确认插入位置）
            int idx = i - 1;
            // 内循环：找到[0,i-1]区间内满足的插入位置，将 base 插入到已排序区间 [0, i-1] 中的正确位置
            while (idx >= 0 && arr[idx] > curKey) { // 如果curKey相对较小则依次往前比较，直到找到第一个合适的位置（此处的while子句实际等价于for循环找位置）
                arr[idx + 1] = arr[idx]; // 将 arr[idx] 向右移动一位
                idx--;
            }
            arr[idx + 1] = curKey;        // 将curKey赋值到正确位置
        }
        // 返回排序后的数组
        return arr;
    }
}